Question

NCERT Solutions Class 12 Maths Chapter 7 Integrals is one of the best study materials for the CBSE board term 1 exam. Our NCERT Solutions is designed by mentors who have years of experience in the field. NCERT Solutions Class 12 also covers various topics of maths such as integrals, integration, etc.

• Integrals – the integrals can be defined as the area under the curve region in a graph. A region bounded by a graph of any function calculated between two points is termed the definite integral of any given function. Intuitively we can see that the bounded region is further divided into thin rectangular areas with the help of lower and upper limits. Then the area is calculated by taking the algebraic sum of the area of the entire region.
• Integration as an Inverse Process of Differentiation – in the differentiation we calculate the derivative of any function while the integration is the process of calculating the antiderivative of a function. So we can say that integration is the inverse process of differentiation.
• Methods of Integration – the method of integration is simply a calculation of adding large values where the general method of algebraic operations is not possible. Hence there are various methods of integration. It is easier to calculate the original integral. There are other different methods of integration
  1. Integration by Substitution.
  2. Integration by Parts
  3. Integration Using Trigonometric Identities
  4. Integration of Some particular function
  5. Integration by Partial Fraction 
• Integration by Partial Fractions – with the help of integration of a partial fraction we can integrate a partial fraction to help integrate a rational fraction integrand that has complex terms of a denominator. We can decompose an expression into many simpler terms which can be used to easily calculate or integrate the expression.

NCERT Solutions Class 12 Maths has in-depth discussions and solutions to all sorts of questions in the related chapter.

Answer 1

153. Integrate the function:

\(sin^{-1} \left(\frac{2x}{1 +x^2}\right)\)

Answer:

Let x = tanθ  

dx = sec²θ dθ

Integrating by parts, we obtain

154. \(\int x^2 e^{x^3}dx \) equals 

(A) \(\frac13 e^{x^3} + C\)

(B) \(\frac13 e^{x^2} + C\)

(C) \(\frac12 e^{x^3} + C\)

(D) \(\frac12 e^{x^2} + C\)

Answer:

Let \(I = \int x^2 e^ {x^3} dx\)

Also, let x³ = t so 3x²dx = dt

Hence, the correct Answer is A.

155. \(\int e^x sec\, x (1 + tan \,x)dx\) equals 

(A) e^xcos x + C

(B) e^xsec x + C

(C) e^xsin x + C

(D) e^xtan x + C

Answer:

\(\int e^x sec\, x (1 + tan \,x)dx\)

Let \(\int e^x sec\, x (1 + tan \,x)dx = \int e^x (sec \, x + sec\, x\;tan\,x)dx\) 

Also, let secx = f(x)  secx tanx = f'(x)

It is known that, 

\(\int e^x [f(x) + f'(x)]dx = e^x f(x) + C\)

\(\therefore I = e^x sec \,x + C\)

Hence, the correct Answer is B.

156. Integrate the function:

\(\sqrt{4 - x^2}\)

Answer:

157. Integrate the function:

\(\sqrt{1 - 4x^2}\) 

Answer:

158. Integrate the function:

\(\sqrt{x^2 + 4x + 6}\)

Answer:

Let

159. Integrate the function:

\(\sqrt{x^2 + 4x + 1}\)

Answer:

Let

160. Integrate the function:

\(\sqrt{1 - 4x - x^2}\)

Answer:

Let

161. Integrate the function:

\(\sqrt{x^2 + 4x -5}\) 

Answer:

Let

162. Integrate the function:

\(\sqrt{1 +3x - x^2}\)

Answer:

Let

163. Integrate the function:

\(\sqrt{x^2 + 3x}\)

Answer:

Let

164. Integrate the function:

\(\sqrt{1 +\frac{x^2}9}\)

Answer:

165. \(\int \sqrt{1 +x^2}\,dx\) is equal to

Answer:

Hence, the correct Answer is A.

166. \(\int \sqrt{x^2 - 8x + 7dx}\) is equal to

Answer:

Let

Hence, the correct Answer is D.

167. Integrate the function:

\(\int\limits^ b_a xdx\)

Answer:

It is known that,

Answer 2

168. Integrate the function:

\(\int^ 1 _{-1} (x + 1)dx\)

Answer:

By second fundamental theorem of calculus, we obtain

169. Integrate the function:

\(\int^3_2\frac1xdx\)

Answer:

By second fundamental theorem of calculus, we obtain

]

170. Integrate the function:

\(\int\limits^2_1(4x^3- 5x^2+ 6x+ 9)dx\)

Answer:

By second fundamental theorem of calculus, we obtain

171. Integrate the function:

\(\int\limits ^\frac\pi4_0sin\,2x\,dx\)

Answer:

By second fundamental theorem of calculus, we obtain

172. Integrate the function:

\(\int\limits ^\frac\pi2_0cos\,2x\,dx\) 

Answer:

By second fundamental theorem of calculus, we obtain

173. Integrate the function:

\(\int\limits^5_4 e^x dx\)

Answer:

By second fundamental theorem of calculus, we obtain

174. Integrate the function:

\(\int\limits^\frac \pi4 _0 tan \, x\; dx\)

Answer:

By second fundamental theorem of calculus, we obtain

175. Integrate the function:

\(\int\limits ^\frac \pi4 _\frac\pi6 cosec \, x\; dx\)

Answer:

By second fundamental theorem of calculus, we obtain

176. Integrate the function:

\(\int\limits ^1_0 \frac {dx}{\sqrt{1 - x^2}}\)

Answer:

By second fundamental theorem of calculus, we obtain

177. Integrate the function:

\(\int\limits^1_0 \frac{dx}{1+ x^2}\)

Answer:

By second fundamental theorem of calculus, we obtain

178. Integrate the function:

\(\int \limits ^3_2 \frac{dx}{x^2 - 1}\)

Answer:

By second fundamental theorem of calculus, we obtain

179. Integrate the function:

\(\int\limits^\frac\pi2_0 cos^2 x\,dx\)

Answer:

By second fundamental theorem of calculus, we obtain

180. Integrate the function:

\(\int\limits^3_2 \frac{xdx}{x^2 + 1}\)

Answer:

By second fundamental theorem of calculus, we obtain

181. Integrate the function:

\(\int\limits^1_0 \frac{2x + 3}{5x^2 + 1}dx\)

Answer:

By second fundamental theorem of calculus, we obtain

182. Integrate the function:

\(\int\limits ^1_0 xe^{x^2}dx\)

Answer:

By second fundamental theorem of calculus, we obtain

Answer 3

183. Integrate the function:

\(\int\limits^\frac\pi4_0 (2sec^2x +x^3 + 2)dx\)

Answer:

By second fundamental theorem of calculus, we obtain

184. Integrate the function:

\(\int\limits ^\pi_0\left(sin^2\frac x2 - cos^2 \frac x2\right)dx\)

Answer:

By second fundamental theorem of calculus, we obtain

185. Integrate the function:

\(\int\limits^2_0\frac{6x + 3}{x^2 + 4}dx\)

Answer:

By second fundamental theorem of calculus, we obtain

186. Integrate the function:

\(\int\limits^1_0\left(xe^x+ sin \frac{\pi x}{4}\right)dx\)

Answer:

By second fundamental theorem of calculus, we obtain

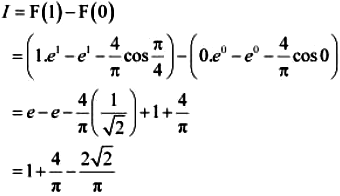
187. \(\int\limits^\sqrt 3_1 \frac{dx}{1 + x^2}\) equals

A. \(\frac \pi3\)

B. \(\frac {2\pi}3\)

C. \(\frac \pi6\)

D. \(\frac \pi{12}\)

Answer:

By second fundamental theorem of calculus, we obtain

Hence, the correct Answer is D.

188. \(\int\limits^\frac23_0 \frac{dx}{4 + 9x^2}\) equals

A. \(\frac \pi6\)

B. \(\frac \pi{12}\)

C. \(\frac \pi{24}\)

D. \(\frac \pi{4}\) 

Answer:

By second fundamental theorem of calculus, we obtain

Hence, the correct Answer is C.

189. Integrate the function:

\(\int\limits ^1_0 \frac x {x^2 + 1}dx\)

Answer:

\(\int\limits ^1_0 \frac x {x^2 + 1}dx\) 

Let x² + 1 = t

⇒ 2x dx = dt

When x = 0, t = 1 and when x = 1, t = 2

190. Integrate the function:

\(\int\limits ^{\frac\pi2}_0\sqrt{sin \phi}\,cos^5 \phi d\phi\)

Answer:

Let \(I=\int\limits ^{\frac\pi2}_0\sqrt{sin \phi}\,cos^5 \phi d\phi=\int\limits ^{\frac\pi2}_0\sqrt{sin \phi}\,cos^4\, cos \phi \,d\phi\) 

Also, let

\(sin \phi = 1 \)

⇒ \(cos\phi\, d\phi = dt\)

191. Integrate the function:

\(\int\limits^1_0 sin^{-1} \left(\frac{2x}{1 +x^2}\right)dx\)

Answer:

Let \(I=\int\limits^1_0 sin^{-1} \left(\frac{2x}{1 +x^2}\right)dx\) 

Also, let x = tanθ ⇒ dx = sec²θ dθ 

When x = 0, θ = 0 and when x = 1, \(\theta = \frac\pi4\)

Taking θ as first function and sec²θ as second function and integrating by parts, we obtain

192. Integrate the function:

\(\int\limits_0^2 x \sqrt{x + 2} \,(\text{Put } x + 2= t^2)\)

Answer:

\(\int\limits_0^2 x \sqrt{x + 2dx} \) 

Let x + 2 = t² 

⇒ dx = 2tdt 

When x = 0, t = √2 and when x = 2, t = 2

193. Integrate the function:

\(\int \limits^\frac\pi2_0 \frac {sin\, x}{1 + cos^2 x}dx\)

Answer:

\(\int \limits^\frac\pi2_0 \frac {sin\, x}{1 + cos^2 x}dx\)

Let cos x = t 

⇒ −sinx dx = dt 

When x = 0, t = 1 and when \(x = \frac\pi2, t = 0\)

194. Integrate the function:

\(\int\limits^2_0 \frac{dx}{x + 4 - x^2}\)

Answer:

Let \(x - \frac12 = t\) So dx = dt

Answer 4

195. Integrate the function:

\(\int\limits ^1_{-1}\frac{dx}{x ^ 2 + 2x + 5}\)

Answer:

Let x + 1 = t ⇒ dx = dt 

When x = −1, t = 0 and when x = 1, t = 2

196. Integrate the function:

\(\int\limits^2_1 \left(\frac 1x - \frac1{2x^2}\right)e^{2x}dx\)

Answer:

\(\int\limits^2_1 \left(\frac 1x - \frac1{2x^2}\right)e^{2x}dx\)

Let 2x = t ⇒ 2dx = dt 

When x = 1, t = 2 and when x = 2, t = 4

197. The value of the integral is \(\int\limits^1_{\frac13} \frac{(x - x^3)^\frac13}{x^4}\) is

A. 6

B. 0

C. 3

D. 4

Answer:

Let \(I =\int\limits^1_{\frac13} \frac{(x - x^3)^\frac13}{x^4}\) 

Also, let x = sinθ ⇒ dx = cosθ dθ

Let cotθ = t ⇒ −cosec²θ dθ= dt

Hence, the correct Answer is A.