Question

Inside a triangular park, there is a flower bed forming a similar triangle. Around the flower bed runs a uniform path of such a width that the sides of the park are exactly double of the corresponding sides of the flower bed. The ratio of the area of the path to the flower bed is: 

(a) 1 : 1 

(b) 1 : 2 

(c) 1 : 3 

(d) 3 : 1

Answer 1

(d) 3 : 1

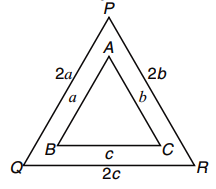
Let ABC be the triangular flower bed of side lengths a, b and c respectively. Then 

Area of ΔABC = \(\sqrt{s(s-a)(s-b)(s-c)}\)

where s = \(\frac{a+b+c}{2}\)

Now according to the given condition,

ΔPQR forms the park with side lengths 2a, 2b, 2c.

∴ Area of ΔPQR = \(\sqrt{s'(s'-2a)(s'-2b)(s'-2c)}\)

where s' =\(\frac{2a+2b+2c}{2}\) = a + b + c = 2s

∴ Area of ΔPQR = \(\sqrt{2s(2s-2a)(2s-2b)(2s-2c)}\)

= 4 \(\sqrt{s(s-a)(s-b)(s-c)}\)

= 4. Area of ΔABC.

∴ Area of path =  Area of ΔPQR - Area of ΔABC

= 4 x Area of ΔABC - Area of ΔABC

= 3 (Area of ΔABC)

∴ Reqd. Ratio = Area of Path : Area of ΔABC = 3 : 1.