Examine the continuity of the function f(x) = { (|x| +3, x≤-3)(-2x, -3<x<3)(6x+2, x≥3)

Question

Examine the continuity of the function

\(f(x)= \begin{cases} |x|+3,& \quad x≤-3\\ -2x,& \quad -3<x<3\\ 6x + 2,& \quad x≥3 \end{cases} \)

Answer 1

In the intervals x ≤ -3, f(x) is the sum of a constant function and modulus function so continuous. In the intervals -3 < x < 3 and x ≥ 3the function f(x) is a polynomial so continuous. Hence we have to check the continuity at x = -3, x = 3.

At x = -3

f(-3) = 6

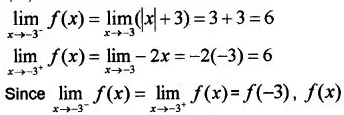
f(x) is continuous at x = -3.
At x = 3
f(3) = 6(3) + 2 = 20

Since lim_x→3⁻f(x) = f(3), f(x) is not continuous at x = 3.