Show that the lines vector(r) = 3i + 2j - 4k + λ(i + 2j + 2k);

Question

Show that the lines

\(\vec{r}=3\hat{i}+2\hat{j}-4\hat{k}+ \lambda (\hat{i}+2\hat{j}+2\hat{k});\)

\(\vec{r}=5\hat{i}-2\hat{j}+ \mu (3\hat{i}+2\hat{j}+6\hat{k});\)

are intersecting. Hence find their point of intersection.

Answer 1

Given lines are

\(\vec{r}=3\hat{i}+2\hat{j}-4\hat{k}+ \lambda (\hat{i}+2\hat{j}+2\hat{k})\) and \(\vec{r}=5\hat{i}-2\hat{j}+ \mu (3\hat{i}+2\hat{j}+6\hat{k})\)

Its corresponding cartesian forms are

If two lines (i) and (ii) intersect, let interesting point be.

\(\Rightarrow\) \((\alpha, \beta, \gamma)\) satisfy line (i)

Also, \((\alpha, \beta, \gamma)\) will satisfy line (ii)

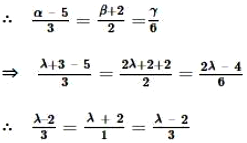
\(\therefore\) The value of 1 is same in both cases.

Hence, both lines intersect each other at point