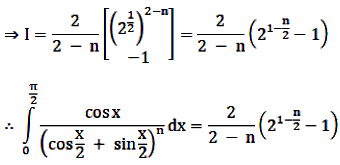Let I = \(\int\limits_{0}^{\pi/2}\cfrac{cos\,\text x}{(cos\frac{\text x}2+ sin\frac{\text x}2)^n}d\text x \)
We can write,

Put cos\(\cfrac{\text x}2\) + sin\(\cfrac{\text x}2\) = t
⇒(-\(\cfrac12\) sin\(\cfrac{\text x}2\) +\(\cfrac12\)cos\(\cfrac{\text x}2\)) dx =dt
(Differentiating both sides)
⇒( cos\(\cfrac{\text x}2\) - sin\(\cfrac{\text x}2\) )dx = 2dt
When x = 0, t = cos 0 + sin 0 = 1
When x = \(\cfrac{\pi}2 \), t = cos\(\cfrac{(\frac{\pi}2)}2 \) + sin \(\cfrac{(\frac{\pi}2)}2 \)
= \(\cfrac{1}{\sqrt2}\) + \(\cfrac{1}{\sqrt2}\) = \(\sqrt2\)
So, the new limits are 1 and \(\sqrt2\).
Substituting this in the original integral,