Question

The bag A contains 8 white and 7 black balls while the bag B contains 5 white and 4 black balls. One balls is randomly picked up from the bag A and mixed up with the balls in bag B. Then a ball is randomly drawn out from it. Find the probability that ball drawn is white.

Answer 1

Given:

Bag A contains 8 white and 7 black balls

Bag B contains 5 white and 4 black balls.

A ball is transferred from bag A to bag B and then a ball is drawn from bag B.

There are two mutually exclusive ways to draw a white ball from bag B –

a. A white ball is transferred from bag A to bag B, and then, a white ball is drawn from bag B

b. A black ball is transferred from bag A to bag B, and then, a white ball is drawn from bag B 

Let E₁ be the event that white ball is drawn from bag A and E2 be the event that black ball is drawn from bag A.

Now, we have

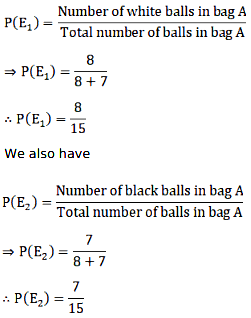
Let E₃ denote the event that white ball is drawn from bag B.

Hence, we have

Using the theorem of total probability, we get

P(E₃) = P(E₁)P(E₃|E₁) + P(E₂)P(E₃|E₂)

Thus, the probability of the drawn ball being white is \(\cfrac{83}{150}.\)