Question

Find the locus of the mid-points of the portion of the line x sinθ + y cos θ = p intercepted between the axes.

Answer 1

Given: 

Line x sin θ + y cos θ = p 

To find: 

The locus of the mid-points of the portion of the line x sinθ + y cos θ = p intercepted between the axes. 

Explanation: 

If the equation of the given line is x sin θ + y cos θ = p, then the solution is shown below: 

The line x sin θ + y cos θ = p intercepts the axes. 

Thus, the coordinate of the point where the line intercepts x – axis is  \(\Big(\frac{P}{cosθ},0\Big)\) 

Thus, the coordinate of the point where the line intercepts y – axis is \(\Big(0,\frac{P}{sinθ}\Big)\) 

 The midpoint R of the line is given by 

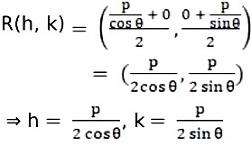
Eliminating the sine and cosine terms, we get

⇒ p²(h² + k²) = 4h²k²

Thus, the locus is given by 

p²(x² + y²) = 4x²y²