Question

A road roller of 200 kg wt slides on ground when pushed by a lever AB of length 1m, as shown in the figure. The force required to slide the roller acts at a distance of 5cm from the fulcrum. If the coefficient of friction between the roller and the ground is `sqrt(2)` find the effort required to move the roller. (Take ` g= 10 m s^(-2)`)

Answer 1

The various forces acting on the road roller are shown below in figure.
Let the force required to slide the roller be F. The component of the force F, to overcome the force of friction `f_(s)` is
`F cos theta = F cos theta 45^(@)=(F)/(sqrt(2)) " " (1)`

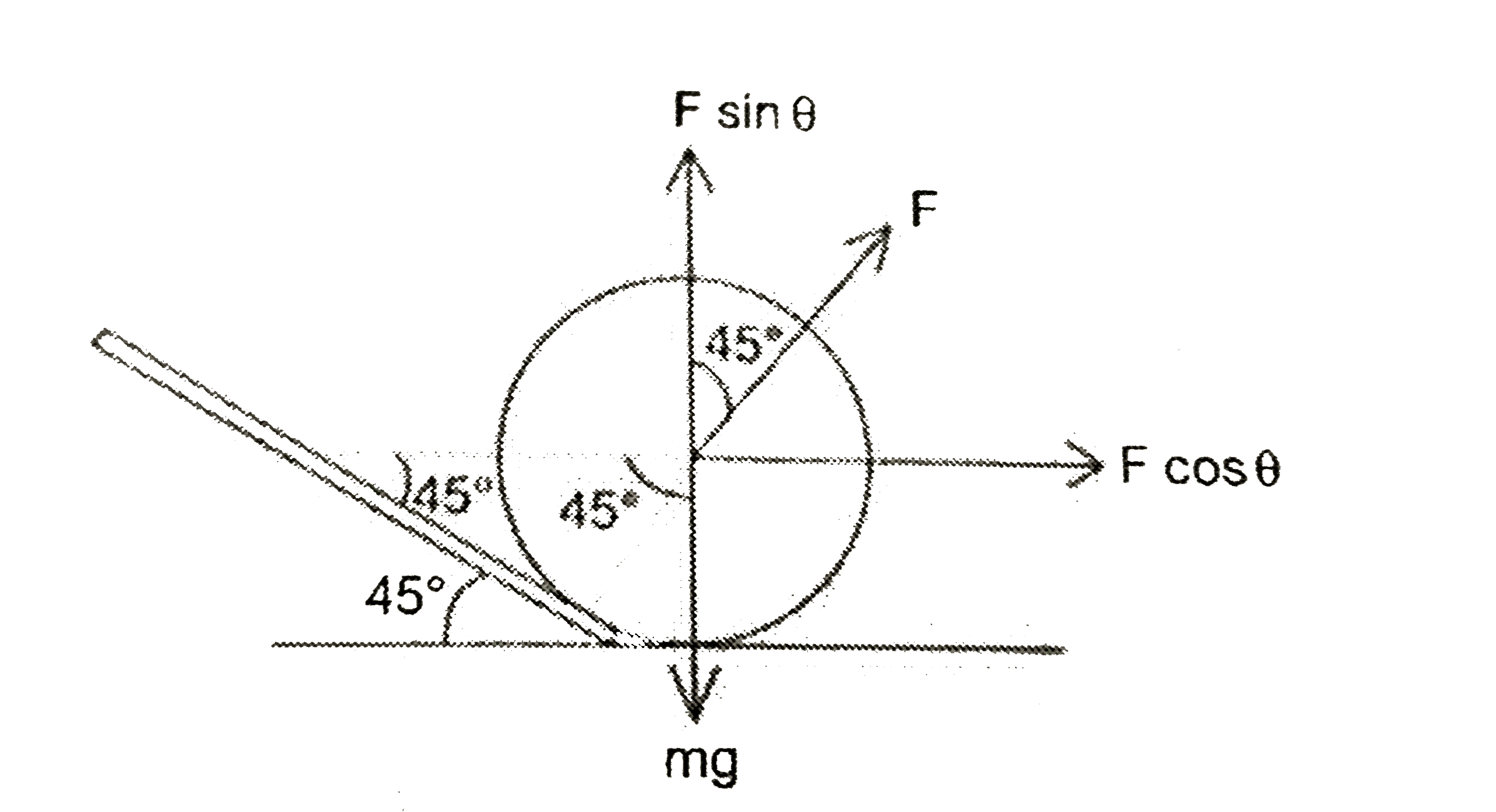
The force of friction `f_(s)= mu N ` where` N = mg - F sin theta`
substituting mg `=200xx10=2000 N`
` sin theta = sin = 45^(@)`
`N= 2000 -(F)/(sqrt(2))`
The frictional force `f_(s)`
`f_(s)= mu N = sqrt(2)xx(200-(F)/(sqrt(2)))`
`f_(s)=2000 sqrt(2)-F " " (2)`
Equationg (1) and (2)
`(F)/(sqrt(2))=2000 sqrt(2)-F`
`F=4000-sqrt(2)F`
`F=(4000)/(sqrt(2)+1)=(4000)/(sqrt(2)+1)xx(sqrt(2)-1)/(sqrt(2)-1)`
`=4xx414=1656N`
Applying the law of moments to the lever,
E `xx` effort arm = load `xx` load arm
`Exx1= 1656 xx 0.05`
`E=82.8 N ~= 83 N` (approximately)