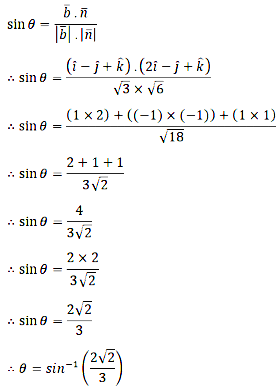Given :
Equation of line : \(\bar{r}\) = (\(\hat{i}\) + \(\hat{j}\) - 2\(\hat{k}\)) + λ ( \(\hat{i}\) - \(\hat{j}\) + \(\hat{k}\))
Equation of plane : \(\bar{r}\) = (2\(\hat{i}\) - \(\hat{j}\) + \(\hat{k}\)) = 4.
To Find : angle between line and plane
Formulae :
1) Angle between a line and a plane :
If Ө is a angle between the line \(\bar{r}\) = \(\bar{a}\) + λ\(\bar{b}\) and the plane \(\bar{r}\).\(\bar{n}\) = p, then
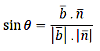
Where, \(\bar{b}\) is vector parallel to the line and
\(\bar{n}\) is the vector normal to the plane.
Answer :
For given equation of line,

Parallel vector to the line is

Therefore, angle between given line and plane is