Question

A man 1.8 metre tall standing at the top of a telephone tower, saw the top of a 10-metre high building at a depression of 40° and the base of the building at a depression of 60°. What is the height of the tower? How far is it from the building?

Answer 1

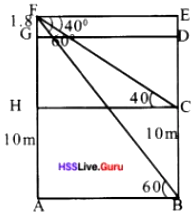
Height of the building = 10m

Height of the towerAG

Height of the man GF = 1.8m

AB = x

In the right triangle CHF tan 40 = \(\frac{HF}{x}\)

HF = x tan 40

= x × 0.8391

= 0.8391x

In the right ABF tan 60 = \(\frac{AF}{AB}=\frac{AF}{x}\)

⇒ AF = x tan 60 = 1.732x

BC = AH = AF – HF

= 1.732x – 0.8391x = 10

= o.8929x = 10

\(x=\frac{10}{0.8929}=11.2\)

= AF = 1.732 x 11.2 = 19.4

Height of tower = 19.4 – 1.8 =17.6 m

Distance from building to tower = 11.2m