Consider a narrow cylindrical pipe of length l closed at one end. When sound waves are sent down the air column in a cylindrical pipe closed at one end, they are reflected at the closed end with a phase reversal and at the open end without phase reversal. Interference between the incident and reflected waves under appropriate conditions sets up stationary waves in the air column.
The stationary waves in the air column in this case are subject to two boundary conditions that there must be a node at the closed end and an antinode at the open end.
Taking into account the end correction e at the open end, the resonating length of the air column is L = l + e.
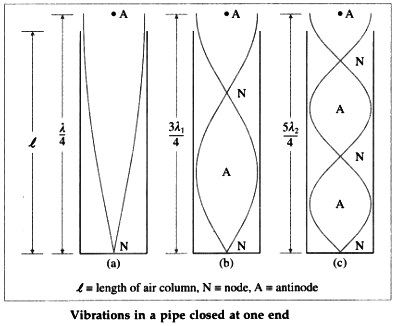
Let v be the speed of sound in air. In the simplest mode of vibration, there is a node at the closed end and an antinode at the open end. The distance between a node and a consecutive anti-node is \(\lambda\)/4, where λ is the wavelength of sound. The corresponding wavelength λ and frequency n are

This gives the fundamental frequency of vibration and the mode of vibration is called the fundamental mode or first harmonic.
In the next higher mode of vibration, the first overtone, two nodes and two antinodes are formed. The corresponding wavelength λ1 and frequency n1 are

Therefore, the frequency in the first overtone is three times the fundamental frequency, i.e., the first overtone is the third harmonic.
In the second overtone, three nodes and three antinodes are formed. The corresponding wavelength λ1 and frequency n2 are

which is the fifth harmonic. Therefore, in general, the frequency of the pth overtone (p = 1, 2, 3, ,..) is np = (2p + 1)n … (4)
i.e., the pth overtone is the (2p + 1)th harmonic.
Equations (1), (2) and (3) show that allowed frequencies in an air column in a pipe closed at one end are n, 3n, 5n, …. That is, only odd harmonics are present as overtones.