- Spherical mirrors:
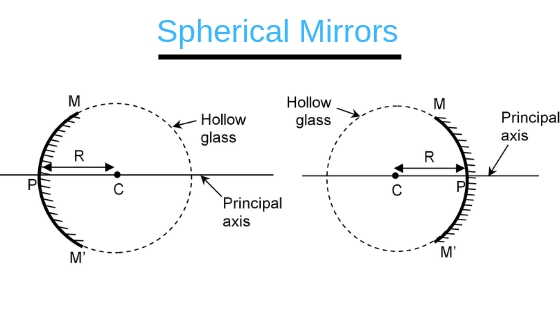
- Any mirror which has curved reflecting surface are spherical mirrors.
- Spherical mirror is a part of a sphere.
Types of spherical mirrors:
There are two types of spherical mirrors:
Concave mirror:
- A spherical mirror whose reflecting surface is curved inwards is said to be concave mirror.
- It is also called converging mirror as it converges parallel beam of light falling on it.
Convex mirror
- A spherical mirror whose reflecting surface is curved outwards is said to be convex mirror.
- It is also called diverging mirror as it diverges parallel beam of light falling on it.
Terminology related to spherical mirrors:
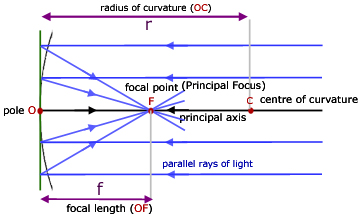
To read light reflection and refraction we must be aware of some common terminology. They are:
- Principal axis: Pole and center of curvature is joined by a line called principal axis.
- Pole: The center of the mirror is pole. We denote it by ‘P’.
- Aperture: The effective length of the mirror is aperture.
- Center of curvature: The center of the sphere which mirror is a part is center of curvature. It is denoted by ‘C’.
- Radius of curvature: The radius of the sphere which mirror is a part is radius of curvature.
- Focus: When parallel light beam is incident on the spherical mirror, then after reflection, the point at which they meet or appears to meet is said to be focus of that mirror.
- Focal length: The length of the line joining pole and focus of the spherical mirror is its focal length. It is denoted by the symbol ‘f’.
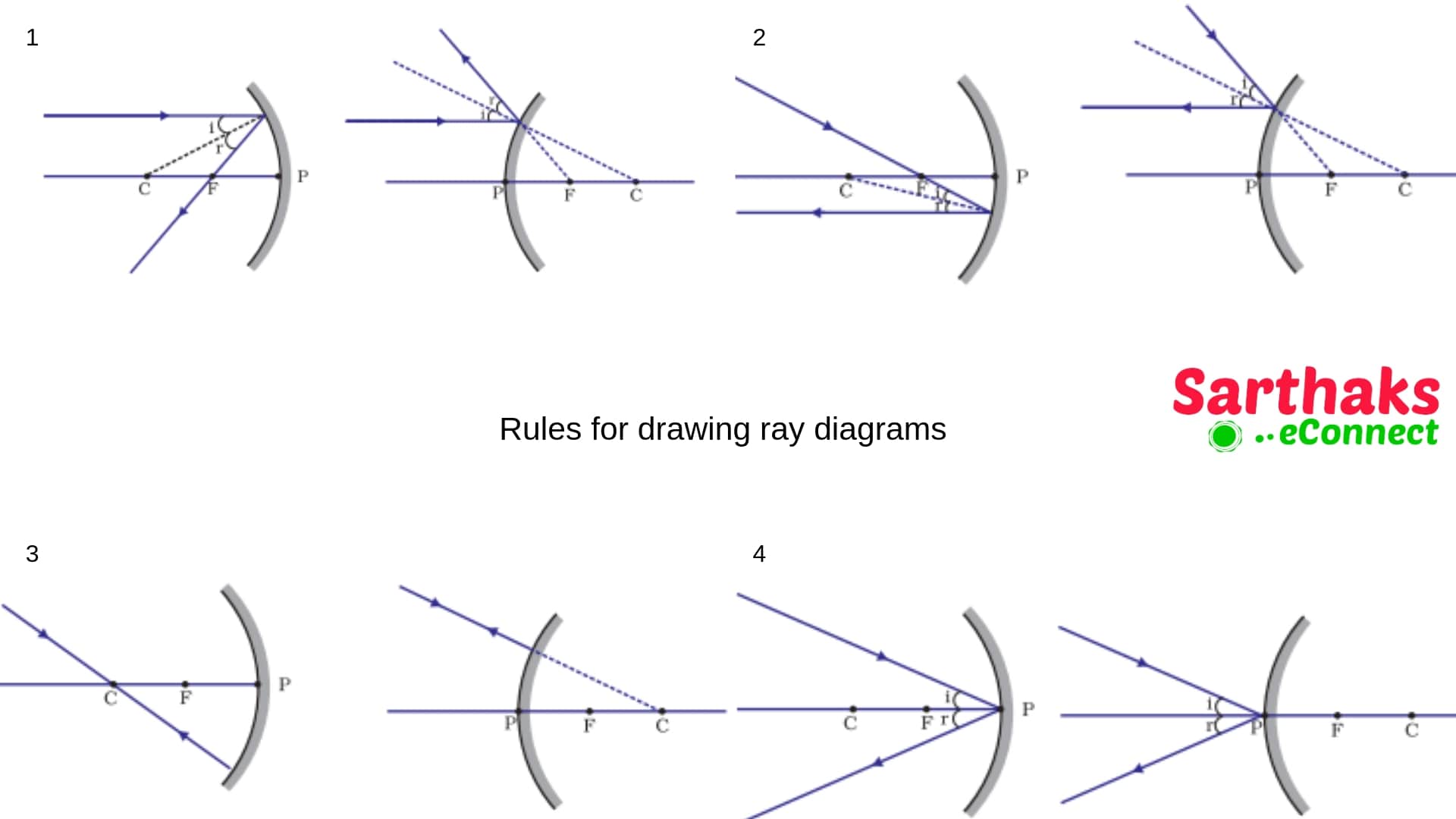
Ray diagram:
There are certain rules we should follow to make ray diagrams which will further used in understanding light reflection and refraction.
- A beam of parallel rays incident on spherical mirror after reflection passes through focus. In case of concave mirror the reflected ray converges to focus but in case of convex mirror the ray appears to diverge from focus.
- The incident ray when passes through focus after reflection it passes parallel to the principal axis.
- A ray incident on the spherical mirror passing through center of curvature returns back on same path.
- A ray incident to the pole of the mirror after reflection makes equal angle with the principal axis.
Images formed by concave mirror:
Here are the ray diagrams for images formed by concave mirror when object is kept at different position with respect to the concave mirror:
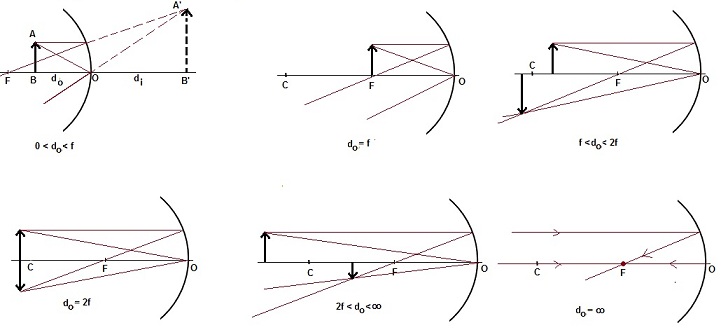
| Position of object |
Position of image |
Nature of image |
Size of image |
| At infinity |
At Focus ‘F’ |
Real & inverted |
Point sized |
| At far from ‘C’ |
between ‘F’ and ‘C’ |
’’ |
Diminished |
| At ‘C’ |
At ‘C’ |
’’ |
Same size as object |
| B/w ‘F’ & ‘C’ |
Far from ‘C’ |
’’ |
Enlarged |
| At Focus ‘F’ |
At infinity |
’’ |
Highly enlarged |
| B/w ‘P’ & ‘F’ |
Behind the mirror |
Virtual & Erect |
Enlarged |
Uses of concave mirror:
- It is used in search lights, vehicle headlights, torch.
- We use it as a shaving mirror.
- It is used by doctors (dentists) to see the enlarged image of the teeth.
- In solar furnace large concave mirrors are used to converge solar heat at a single point.
Images formed by convex mirror:
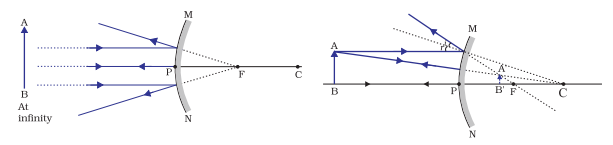
| Position of object |
Position of image |
Nature of image |
Size of image |
| At infinity |
At Focus ‘F’ |
Virtual & Erect |
Point sized |
| B/w pole and infinity |
between ‘P’ and ‘F’ |
’’ |
Diminished |
Uses of convex mirror:
- Convex mirror is used as the rear view mirror as it covers wide view and the image is always erect.
- In shops it is used as the security mirror. Now CCTV does the same.
- At danger traffic turns it is used to see the opposite comers.
Sign convention used in spherical mirror:
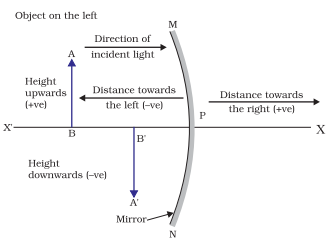
These observable conventions will help you in solving numerical related to light reflection and refraction.
- Object is always placed to the left of mirror.
- All distance are measured from pole of the mirror.
- Distances which are measured in the direction of incident ray are positive.
- Distances which are measured in the opposite direction of incident ray are n
- All distances measured above the principal axis along y-axis are positive.
- Distances measured below the principal axis along negative y-axis are negative.
Note: Object distance (U) is always negative, focal length of concave mirror is negative where convex mirror is positive.
Mirror formula:
The mirror formula in which v is the image distance, u is the object distance, and f is the focal length is given by:
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\)
Magnification formula:
Magnification is the ratio of height of image to that of the object. It will take each case of light reflection and refraction either in mirror or lens.
m = \(\frac{Height\:of\:image}{Height\:of\:object} = \frac{h_i}{ h_o}\)
Also, m = \(\frac{-v}{u}\)
Rules based on magnification:
- If m is negative then image is real but when it is positive then image is virtual.
- If hi = ho then m = 1, i.e. image is equal to the object, if hi > ho then m >1 image is enlarged also if hi < ho then m<1 image is diminished.
- Magnification of plane mirror is always +1.
- If m is +ve and less than 1 then it is convex mirror.
- If m is +ve and more than 1 also when m<1 then it is concave mirror.
Refraction:

The bending of light when it passes from one medium to other is said to be refraction of light.
By this we can distinguish light reflection and refraction.
Glass slab experiment:
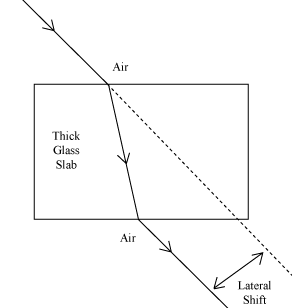
- When there is one different medium (glass slab) between two same medium and the light bending will be parallel to the incident ray.
- The distance between these two lines are called lateral displacement.
- Lateral displacement depends upon thickness and refractive index of the glass slab.
Laws of refraction:
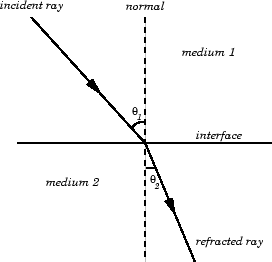
- The incident ray, the refracted ray and normal to the interface of two transparent media at the point of incidence all lies in the same plane.
- The ratio of sine of angle of incidence to the sine of angle of refraction is always constant, for a light of given colour and for a given media. This law is also called Snell’s law.
\(\frac{sin θ_1}{sin θ_2} = constant\)