Question

In the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle `theta` with the horizontal floor. The coefficient of friction between the wall and the ladder is `mu_1` and that between the floor and the ladder is `mu_2.` the normal reaction of the wall on the ladder is `N_1` and that of the floor is `N_2.` if the ladder is about to slip. than

A. `mu_(1)=0, mu_(2) ne 0and N_(2) tan theta = mg//2`
B. `mu_(1) ne 0, mu_2 = 0 and N_(1) tan theta = mg//2`
C. `mu_(1) = 0,mu_(2) ne 0 and N_(2) = (mg)/(1 + mu_(1) mu_(2))`
D. `mu_(1) = 0,mu_(2) ne 0 and N_(1) tan theta = (mg)/(2)`

Answer 1

Correct Answer - c,d
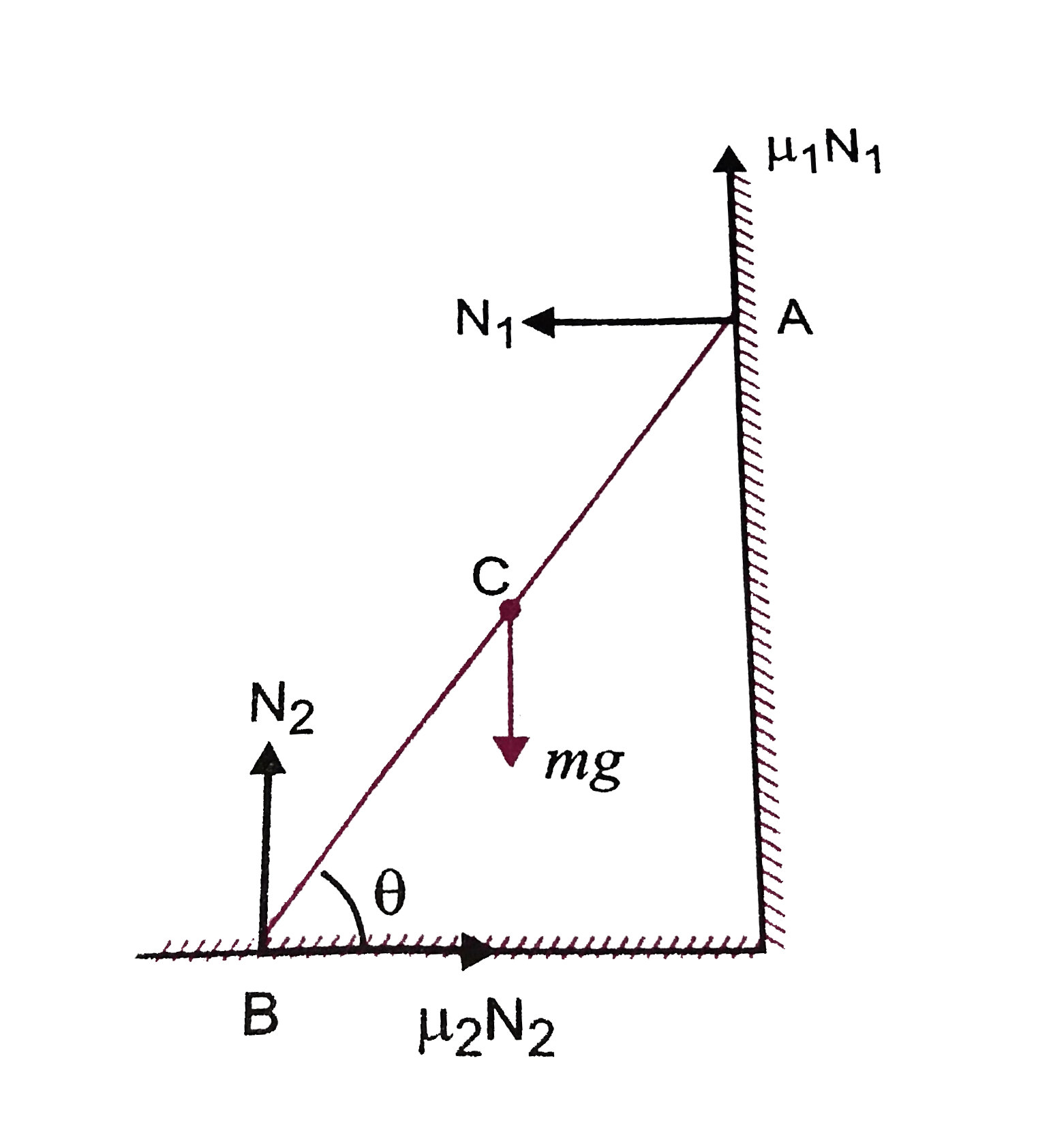
Shown here For static equilibrium `m_(2)` can never be zero When `mu_(1) =0` then
`N_(1) =mu_(2) N_(2)`…(i)
and `N_(2) = mg`…(ii)
As ladder is in equilibrium so taking moments of forces about point `B` we have
`mg (L)/(2) cos theta =N_(1) L sin theta`
or `N_(1) = (mg)/(2tan theta)` or `N_(1) tan theta = (mg)/(2)`
When `mu_(1) ne 0` and there is equilibrium of ladder
then `mu_(1) N_(1) + N_(2) =mg`...(iii)
and `mu_(2) N_(2) = N_(1)` ...(iv)
putting (iv) in (iii) we get
`mu_(1) mu_(2) + N_(2) = mg` or `N_(2) = (mg)/(1 + mu_(1) mu_(2)`
.