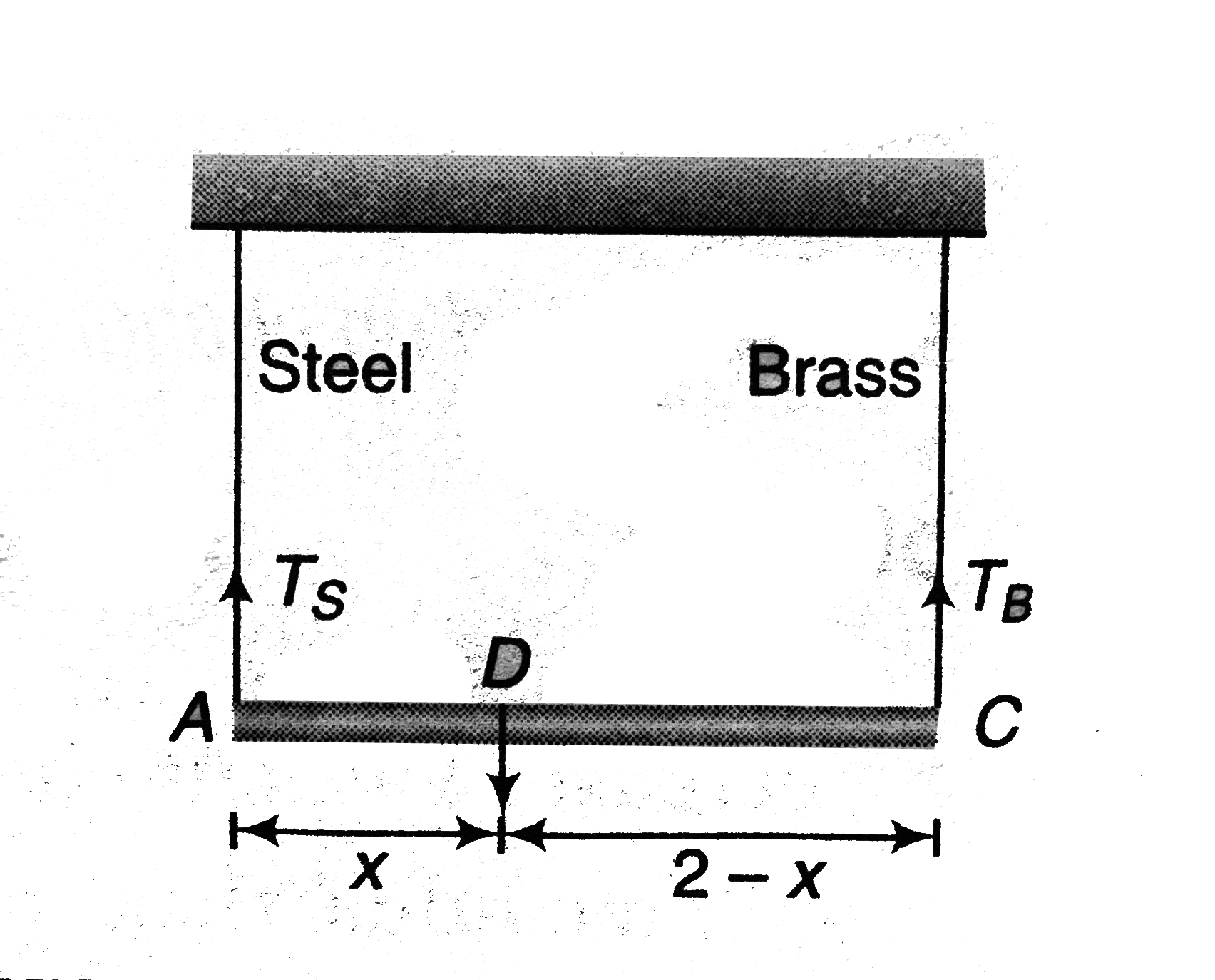Question

A light rod of length of length `2 m` is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section `10^(-3) m^(2)` and the other is of brass of cross- section `2xx10^(-3) m^(2).x` is the distance from the steel wire end, at which a weight may be hung. ` Y_(steel) = 2xx10^(11) Pa and Y_(brass) = 10^(11) Pa`
Which of the following statement(s) is /are correct ?

Answer 1

Correct Answer - A::B::C
(a) Given, stress in steel =stress in brass
` T_(s)/A_(s)=T_(B)/A_(B )`
`T_(s)/T_B=A_(S)/A_(B)`
=`10^(-3)/(2xx10^(-3)) =1/2 `…(i)
As the system is in equilibrium, taking moments about D, we have
`T_(s.x)=T_(B)(2-x)`
:.` (T_(S))/(T_(B))=(2-x)/x ` .....(ii)
From Eq_s.(i) and (ii), We get `x=1.33m`
(b) `"Strain" = "stress"/Y`
Given, strain in steel = strain in brass
`:.(T_(s)//A_(s))/Y_(s)=(T_(B)//A_(B))/(Y_(B))`
`:.T_(S)/T_(B) =(A_(s)Y_(s))/(A_(B)Y_(B))=((1xx10^(-3))(2xx10^11))/((2xx10^(-3))(10^(11)) =1` .....(iii)
from Eq_s.(ii) and (iii), We have `x=1.0 m`