Newton’s Second law of motion:
- According to Newton’s second law of motion, the rate of change of momentum of an object is directly proportional to the applied unbalanced force in the direction of the force.
- Momentum: The product of mass and velocity is called momentum.
- It is a vector quantity and has direction same as the velocity of the object.
- Momentum is denoted by ‘p’.
- It’s SI unit is Kg metre/second.
- Thus equation of Momentum is “p = mv”, where m is mass of the object and v is associated velocity.
- Stationary body has zero momentum.
- 1 N force: When acceleration of 1m/s2 is produced on 1kg object then it is said that 1 N force is applied.
Application of Newton’s second law of motion:
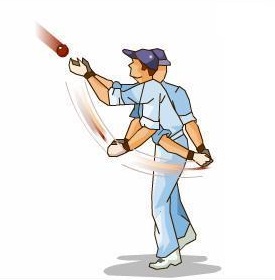
- A cricketer when catches a ball moves his hand backwards in the direction of ball to decrease the velocity of the ball. If he would catch the ball without moving his hand it will require a greater force, This leads to drop of catches.
Mathematical formulation of Second law of motion:
Let the mass of any object be m and its initial velocity is u in a straight line. After time t with a constant acceleration a the object reaches to final velocity v.
- Initial momentum of the body: P1 = m x u
- Final momentum of the body: P2 = m x v
- Change in momentum; P2 – P1 = m(v-u)
- As per the second law of motion the rate of change of momentum is directly proportional to the applied force.
F ∝ m(v – u)/t
F ∝ ma since acceleration is rate of change of velocity (i.e (v – u)/t)
F = K ma where K is the proportionality constant.
1 unit force = K × (1 kg) × (1 m/s2), the value of K becomes 1.
Thus, F = ma
- The SI unit of force is N (i.e. Kg m/s2).
- By the use of Newton’s Second law of motion we can find the force acting on any object.
Newton’s third law of Motion:
- To every action, there is an equal and opposite reaction.
- In other words, when a body exerts a force on another body, the second body instantly exerts a force of equal magnitude to the applied force back onto the first body. These forces are always opposite in direction and act on two different objects always.
- Force has same magnitude acting on each other but may or may not have equal acceleration.
- As, when a bullet is fired from a gun, Bullet moves with high speed but the gun moves a little back. This occurs due to a large difference in mass of the bullet as well as the gun.

Applications of Newton’s Third law:
- Helps in walking.
- It also helps in hitting a goli ball.
- Helps skydivers
- Newton’s third law has a great application in aerodynamics.
What is the law of conservation of momentum?
- According to the law of conservation of momentum, the sum of momenta of two objects before and after collision remains same given that no external unbalanced force acts upon them.
- Simply we can say that collision conserves the overall momentum of the objects.
- The momentum lost by one object is gained by the other.
Conservation of momentum formula:
- Initial momentum = Final momentum
- If m1 & m2 are the mass of any two object moving with initial velocity u1 & u2 and after collision the velocity became v1 & v2 respectively then conservation of momentum formula is given by:
m1 u1 + m2u2 = m1v1 + m2v2
Conservation of momentum Example (class 9):
Q. How to find the Rate of Change of Momentum?
We can find the rate of change of momentum by simply applying Newton’s second law of motion. According to Newton’s second law of motion the rate of change of momentum is directly proportional to the applied force.
Force and laws of motion examples:
Q. A Truck of mass 1200 kg is moving along a straight line with a uniform velocity of 90 km/h. Its velocity is reduced to 18 km/h in 4 s by an unbalanced external force. Calculate the acceleration and change in momentum.
Solution: Mass of the truck, m = 1200 kg
Initial velocity (u) = 90 km/h = 25 m/s
Final velocity (v) = 18 km/h = 5 m/s
Time taken, t = 4 s
According to the first equation of motion:
v = u + at
5 = 25 + a (4)
a = – 5 m/s2
Negative sign indicates that its a retarding motion i.e. velocity is decreasing.
Change in momentum = mv – mu = m (v – u)
= 1200 (5 – 25) = – 24000 kg m s -1
Force = Mass × Acceleration = 1200 × – 5 = – 6000 N
Acceleration of the truck = – 5 m/s2
Change in momentum of the truck = – 24000 kg m s -2
Q. why some of the leaves may get detached from a tree if we vigorously shake its branch?
Solution: When we shake its branches vigorously some leaves get detached because when the branches of a tree are shaken, it moves to and fro, but leaves have tendency to remain at rest. This is because the inertia of the leaves tend to resist the to and fro motion.
Q. How much momentum will a rod of mass 10 kg transfer to the floor if it falls from a height of 80 cm? Take its downward acceleration to be 10 m s-2?
Solution:
Mass of the rod, m = 10 kg
Distance covered by the rod = 80 cm = 0.8 m
Acceleration (a) = 10 m/s2
Initial velocity of the rod, u = 0
Final velocity of the rod = v
According to the third equation of motion:
v2 = u2 + 2as
v2= 0 + 2 (10) 0.8
v= 4 m/s
Hence, the momentum with which the rod hits the floor is = mv
= 40 kg m s-1
Q. A bike of mass 50 kg has a momentum of 1000 kg.m/s. Calculate the velocity of the bike.
Solution: Mass of the body, m = 50 kg
Momentum p = 1000 kg.m/s
p = m x v
v= \(\frac{p}{m}\) = \(\frac{1000}{50}\) = 20 m/s
Hence, the velocity of bike = 20 m/s
Q. Why does a gunman get a jerk on firing a bullet?
Solution: When a bullet is fired from a gun, the force pushing the bullet forward is equal to the force sending the gun back but due to high mass of the gun, it moves only a little distance backwards giving a jerk to the gunman.