Work and Energy Class 9 Science Notes

Question

Revise Work and Energy Class 9 Science Notes for exam.

Answer 1

Important topics covered in work and energy based on NCERT:

• Introduction to work
• What is work?
• Scientific conception of work
• Work done by a constant force
• Energy
• Different forms of energy
• Kinetic energy
• Potential energy
• Inter-conversion of different forms of energy
• Law of conservation of energy
• Commercial unit of energy
• Power (Rate of doing work)

---

What is work?

• When force acting on any object causes displacement then it is said that work is done.
• Work is expressed as the product of force and displacement.
  e. Work done = Force x Displacement = F x S
• Work is a scalar quantity.
• Energy is required to perform work.
• In animals, food supplies the energy whereas in machines fuel supplies the energy to perform work.
• The unit of work is Newton metre or joule.

Funny fact about work and energy:

• If it seems you are working hard and the result came with no work is done as per scientific definition of work.
• Today you have studied throughout the day but scientifically no work is done. I think this made you angry.
• You are pushing a large wall since two hours and wall even not displaced by an inch and you got tired again no work is done.
• At airport you are holding a heavy bag in your hand for half an hour but again scientists say no work is done.

The necessary condition for work done:

• When a moving body stops or comes at rest.
• Stationary object starts moving.
• When there is change in velocity of body.
• Also, when the shape of body changes.

Examples of work done:

• A stationary car moves forward to some distance.
• The running of a child.
• Worker carrying a load to some distance.
• A car moving at 120km/hr stops then there is work done.

Definition of 1 Joule of work:

• When a body is displaced by one metre along the direction of force on applying a force of 1 newton then the work done is 1 joule.
• 1 joule = 1Newton x 1 metre
  1J = 1Nm

Positive, negative and zero work (sign convention):

• When the direction of displacement is same as the force then the work done is said to be positive.
  Example: Pulling a basket by a rope is the example of positive work.
• When direction of displacement is opposite to the direction of force then the work done is said to be negative. Angle between force and displacement is 180⁰.
  Example: A ball rolling on plane stops after some time as the force of friction applies on it in the opposite direction of its displacement, therefore, in this case, negative work is done.
• When there is zero displacement after force is applied then it is said that no work is done or zero work is done. Angle between force and displacement is 0⁰.
  Example: Despite a large amount of force applied on a stationary wall causing no displacement. Thus zero work is done in this case.

The mathematical equation of work:

• If the angle between force and displacement is less than 180⁰ then equation of work is given as:
  W = Fs cosɵ
• Note: {Cos 0⁰ = 1, Cos 90⁰ = 0, Cos 180⁰ = -1).

Factors affecting the amount of work:

• Greater is the force applied greater will be the work done and vice-versa.
• Greater the displacement greater will be the amount of work done.

---

Energy:

• The ability to do work is called energy.
• The energy possessed by anything tells the amount of work it can do.
• The unit of energy is
• Also, 1Kilo-Joule = 1000 Joule
• 1 joule of energy may be defined as the energy required to do 1 joule of work.

Different forms of energy:

In this universe, there are several forms of energy. They are:

• Kinetic energy
• Potential energy
• Chemical energy
• Sound energy
• Light energy
• Heat energy
• Electrical energy

 However, in work and energy class 9 notes, we will read only about kinetic and potential energy.

Answer 2

Kinetic Energy:

• The energy possessed by a body by the virtue of its motion is said to be kinetic energy.
• The kinetic energy of a body increases as the velocity increases.
• A body moving with certain velocity has kinetic energy equal to the energy given to it to attain that velocity.
• Example:
  Moving car is possess kinetic energy.
  A running child.
  A ball after being hit by bat.
  Football when kicked.
  Bullet fired from a gun.
  Water being dropped from a certain height.
  Child sliding.
• Kinetic energy is directly proportional to the mass of body.
• Also, it is directly proportional to square of the velocity possessed by a body.

Derivation of formula of kinetic energy:

• Suppose a body of mass m starts from rest and attains a uniform velocity v after being applied by a force F, during this time the displacement is s. Then
  Work done = F x s ….. (i)
  F = m x a …….. (ii)
  As per the Newton’s third law, it is given that:
  V² – u² = 2as
  S = \(\frac{v^{2} – u^{2}}{2a}\)
  W = \(\frac{1}{2}\) mv² {as the initial velocity is zero}
• But, work done on object = change in its kinetic energy of object
  W = E_k = \(\frac{1}{2}\) mv² – 0 = \(\frac{1}{2}\) mv²

Potential energy:

• The energy possessed by a body due to the virtue of its position is said to be potential energy.
• The potential energy depends upon the height or displacement from base.
• Example:
  Water at a height in the dam has high potential energy which can rotate a large turbine.
  The string of bow with loaded arrow has high potential energy.
  Stretched rubber also have a considerable amount of potential energy due to its distorted shape.

Types of potential energy:

There are two types of potential energy:

1. Gravitational potential energy: The energy possessed by a body by the virtue of its position above the ground.
   Object having a greater height above the ground have more potential energy.
2. Elastic potential energy: The energy possessed by a body due to its change in shape is called elastic potential energy.

Factors affecting Potential energy:

• Mass: More is the mass of object more will be its potential energy and vice versa.
  E ∝ Mass of the object (m)
• Height: More is the height above the ground more will be its potential energy and vice versa.
  E ∝ Height (h)
• Change in Shape: Potential energy increases with bending, stretching, bending, twisting of shape of body.

Equation of potential energy at height:

• Body having mass ‘m’ when lifted to height ‘h’ requires energy.
• Some work is done, as the position acquired is against the gravitational pull of the earth.
• Work done = force x displacement
  W = F x s
  Here, F = mg ..{Here, a = acceleration due to gravity(g) and s = h}
  W = m x g x h = mgh
• The work done on that object is stored as the gravitational potential energy.
• Thus, E_p = mgh
• Height does not depend on the path followed by the object to attain that position.
• g = 9.8 m/s²

Mechanical Energy:

• The sum of kinetic and potential energy is called mechanical energy.
• A bird flying in the air has both kinetic as well as potential energy.

Mechanical energy(ME) = PE + KE
\(\frac{1}{2}\) mv² + mgh

Transformation of energy:

• The change of one form of energy to other form is called transformation of energy.
• Energy can be converted or transformed from one form to another.
• Example:
  When a ball is dropped from some height. At the highest point, the ball has potential energy but as it starts descending potential energy decreases whereas kinetic energy increases. At the point just above the ground, the potential energy becomes zero and the kinetic energy becomes maximum. We can say that its entire potential energy is converted to kinetic energy.
• At hydroelectric power-plant water having a considerable amount of potential energy is converted into kinetic energy. This kinetic energy is used to rotate turbine and thus gets converted into electrical energy.
• At thermal power station, the chemical energy of coal is converted into kinetic energy than into electrical energy.
• In the process of photosynthesis, plants converts solar energy into chemical energy.

Answer 3

Law of conservation of energy:

• According to law of conservation of energy, “energy can neither be created nor be destroyed but can be transformed from one form to another”.
• The total energy before and after the transformation remains the same.
• Although a little amount of energy wasted during the conversion but overall energy of the system remains conserved.

Conservation of energy of a free fall body:

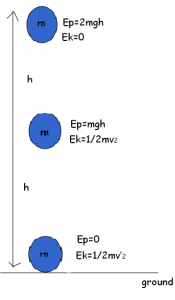
• A ball of mass m at some height h has a potential energy of mgh.
• As it starts falling its potential energy decreases.
• Kinetic energy at height h is ‘0’ but starts increasing during downfall.
• The mechanical energy (i.e. sum of kinetic and potential energy) remains conserved at each point during its fall.

\(\frac{1}{2}\)mv² + mgh = constant

• Kinetic Energy + Potential Energy = Constant

---

Power:

• The rate of doing work is said to be power.
• Simply, we can say that power is the rate of energy consumption.
• The SI unit of power is watt or Joule/Sec.
• 1-watt power may be defined as the power of device which consumes energy of 1 joule in 1 sec.
• Power = \(\frac{Work\:done}{Time\:taken}\) = \(\frac{W}{t}\)
• Average power = \(\frac{total\:work\:done}{total\:time\:taken}\)

Power of an appliance:

• The power of an appliance tells us its rate of consumption of energy.
• We measure power in Kilo Watt at larger scale.
  1 Kilowatt (KW) = 1000 Watt (W or J/s)

Commercial unit of energy:

• In everyday life we use much electricity per day in several means. It is inconvenient to measure the consumption in joule as it is much small amount.
• For commercial purpose we measure electricity consumption in Kilowatt hour (KWh).
• 1 KWh is the amount of energy consumed when an appliance having a rating of power 1 Kilowatt and is used for 1 hour.

Relation between kilowatt hour and Joule/ Mathematical relation between KWh and joule:

• 1 Kilowatt hour (KWh) = 1kilowatt x 1 hour
  1 KWh = 1000W x 3600 sec = 3600000 Joules
  1 KWh = 3.6 x 10⁶ Joules = 1unit

---

Work and Energy Class 9 Examples:

Q. What will cause greater change in kinetic energy of a body? Changing its mass or changing its velocity?

Solution: 
As K.E = \(\frac{1}{2}\) mv² therefore,
K.E ∝ m
K.E ∝ v²
Hence, the change in the velocity of a body will cause a greater change in kinetic energy.

Q. A horse of mass 210 kg and a dog of mass 50 kg are running at the same speed. Which of the two possesses more kinetic energy? How? 

Solution:
Kinetic energy, K.E. = 1/ 2 mv² 
At constant velocity, Kinetic energy is directly proportional to mass. Hence, as mass increases, kinetic energy also increases. In this case, the mass of a horse is greater than that of dog, so the kinetic energy of the horse is greater than the dog when it is given that speed is constant.

Q. If our heart works 60 joules in one minute, find its power? 

Solution:
The power of heart is given by,
Power = work done/time = 60 j / 60 s = 1W. [As Watt (W) = J/s]
Hence power of heart = 1 Watt

When a ball is thrown vertically upwards, its velocity goes on decreasing. What happens to its potential energy as its velocity becomes zero?

Solution:
According to the law of conservation of energy, energy can neither be created nor be destroyed but can be transformed from one form to another.
Therefore, Kinetic energy lost by the ball = Potential Energy gained by the ball
So, as the velocity of the ball becomes zero then K.E would be zero and the P.E. would be maximum.

Comments

Very helpful and simple. Pretty much everything is covered... thank you.