Question

A body of mass `1 kg` initially at rest, explodes and breaks into three fragments of masses in the ratio `1 : 1 : 3`. The two pieces of equal mass fly off perpendicular to each other with a speed of `15 m s^(-1)` each. What is the velocity of the heavier fragment?

Answer 1

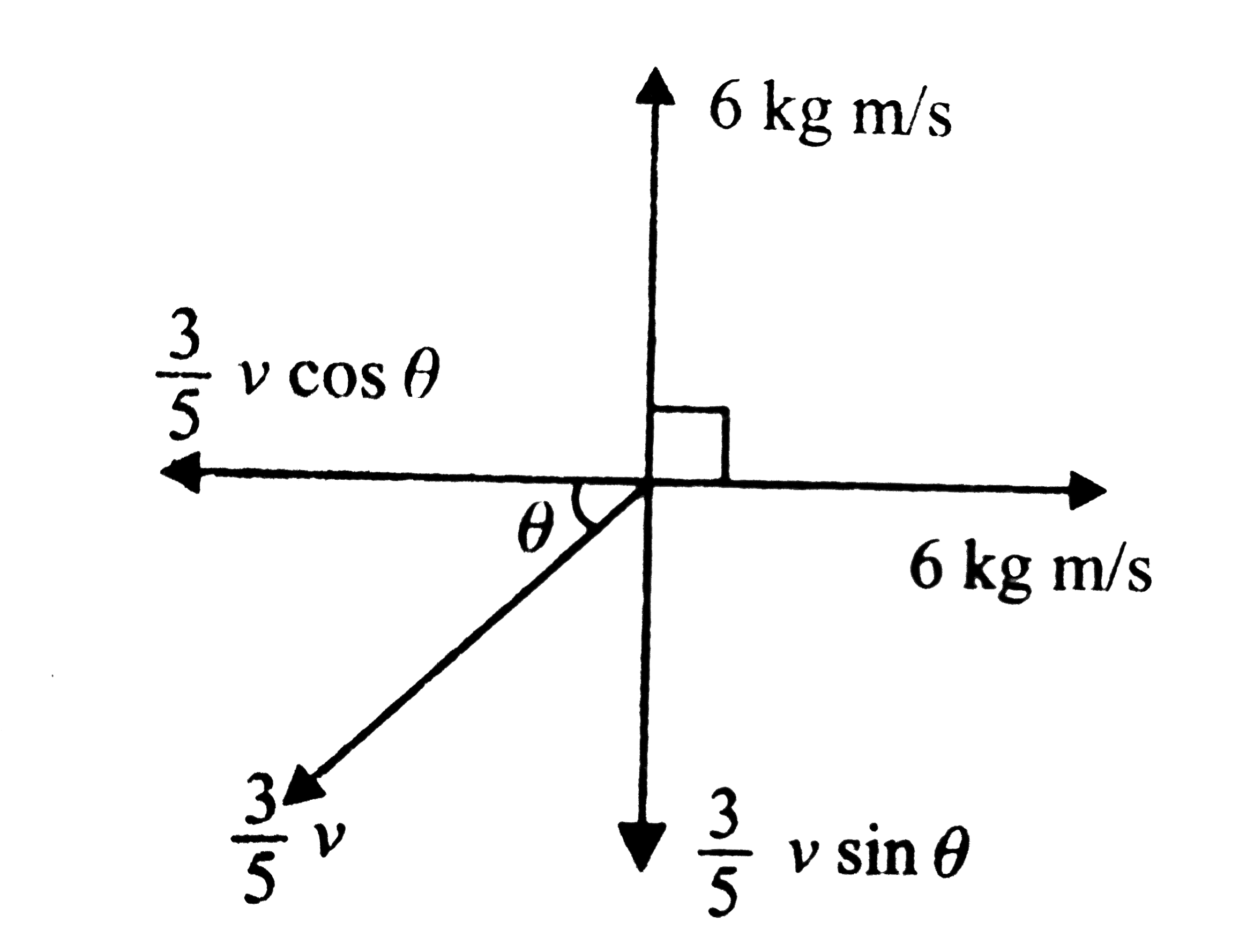
The momentum of the system is zero before explosion. Since the momentum is zero initially, it will be zero just after explosion according to conservation of linear momentum (as there is no external force acting on the system). The resultant momentum of the fragments flying off perpendicular to each other should be equal and opposite to the third fragment. Masses of fragments are `1//5 kg, 1//5 kg` and `3//5 kg`. Momentum of each of the smaller fragments is `1/5xx30=6kgm//s`.
Applying the principle of conservation of linear momentum in both the directions, we get
`6=3/5vsintheta` .............i
`6=3/5costheta` ...................ii
squaring and adding we get `36+36=9/25v^(2)`
`:.v=10sqrt2m//s`
Dividing the two equations, we get
`tantheta=1`, or `theta=45^(@)`