Question

A uniform rod of mass `m=2 kg` and length `l` is kept on a smooth horizontal plane. If the ends `A` and `B` of the rod move with speeds `v` and `2v` respectively perpendicular to the rod, find the:
a. angulr velocity of `CM` of the rod.
b. Kinetic energy of the rod (in Joule).

Answer 1

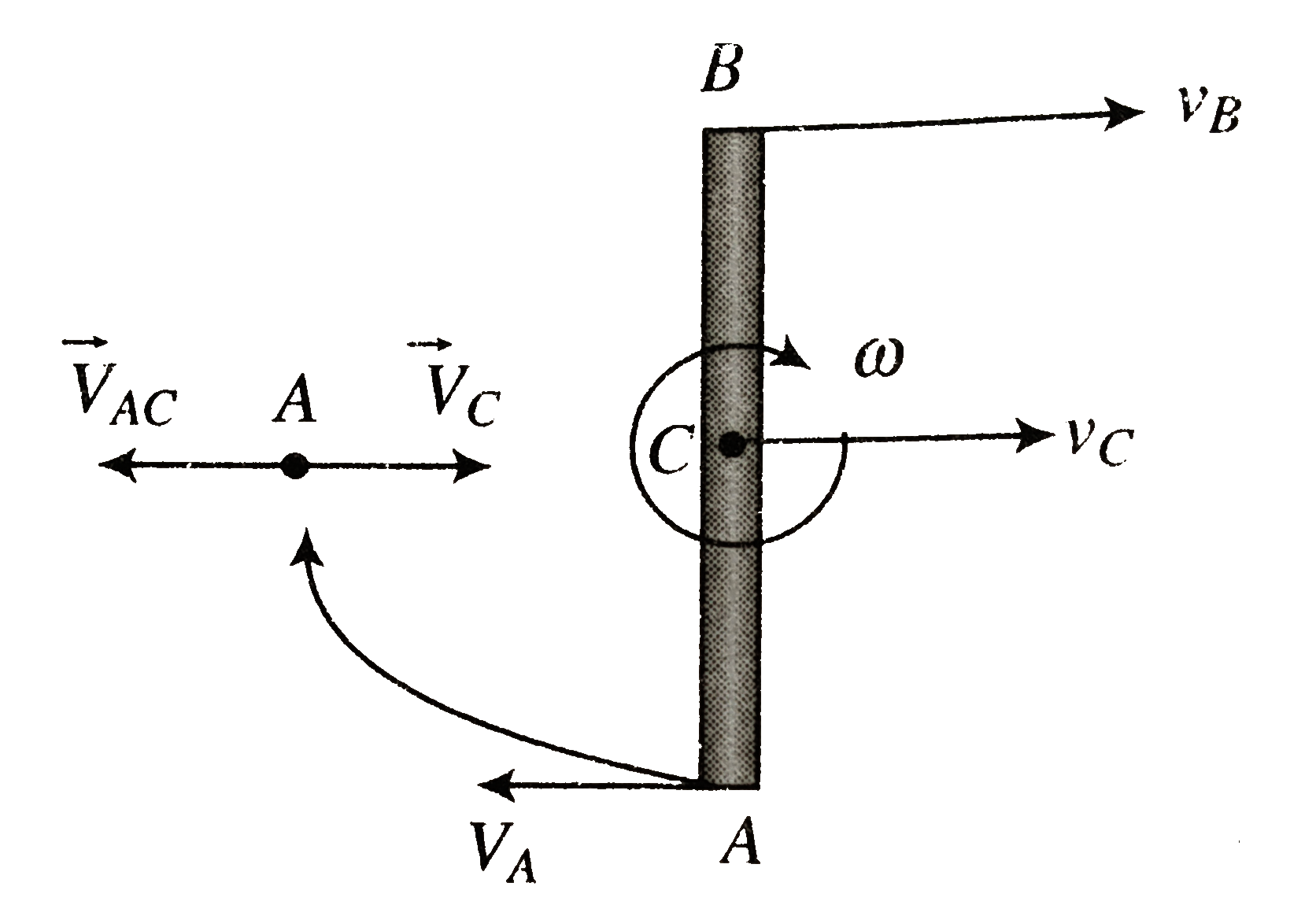
a. As the velocities of the ends `A` and `B` of the rod are given as `2v` and `v` respectively we need to find velocity of centre of mass of rod and its angular velocity as follows:
Since `vecv_(A)=vecv_(AC)=-l/2 omegahati` and `vecc_(C)=vecv_(C)hati`
but we have velocity of `A: v_(A)(=-v)=v_(c)-l/2 omega`..........i
Similarly we have `v_(B)(=2v)=v_(C)+l/2omega`...........ii
solving eqn i and ii we have
`omega=(3v)/l` and `v_(C)=v/2`
b. Then substituting `v_(C)` and `omega` in the equation
`K=1/2mv_(C)^(2)+1/2I_(C)omega^(2)`
we have `K=1/2m(v/2)^(2)+1/2((ml)/2)^(2)((3v)/l)^(2)`
This gives `K=(mv^(2))/2`