Question

A smooth piston of mass `m` area of cross - section A is in equilibrium in a gas jar when the pressure of the gas is `P_(0)`. Find the angular frequency of oscillation of the piston, assuming adiabatic Change of state of the gas.

Answer 1

Correct Answer - ` sqrt((gamma P_(0) A^(2))/(mV_(0)))`
In adabatic procedure, `PV^(gamma) = C`
Taking log of sides, we have log`P + gamma log V = log C`
Taking difference of both sides, we have `(delta P)/(P) + (gamma delta V)/(V) = 0`
This gives the excess presure `Delta P` (where we disturb the position) as
`delta P = (- gamma P)/(V) delta V`
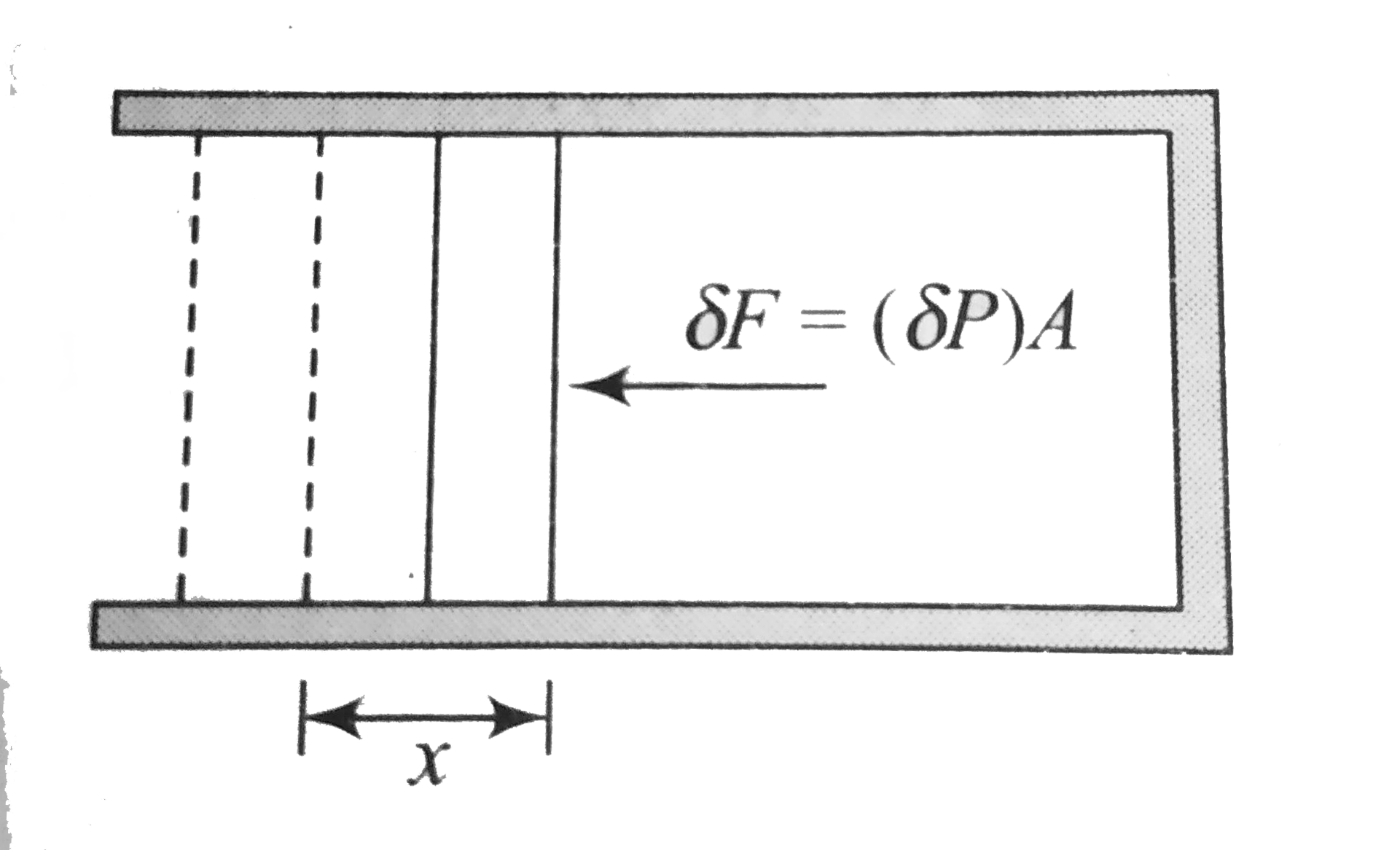
where `Delta V = "charge in valume of the gas" = A Delta x`
Substituting `deltaP = (delta F)/(A), V = V_(0). p = p_(0) and delta V = A delta x`
We have `k_(eff) = [(delta f)/(delta x)] = (gamma P_(0) A^(2))/(V_(0))`
Then, using `omega = sqrt((k_(eff))/(m))`
We have `omega = sqrt((gamma P_(0) A^(2))/(mV_(0)))`