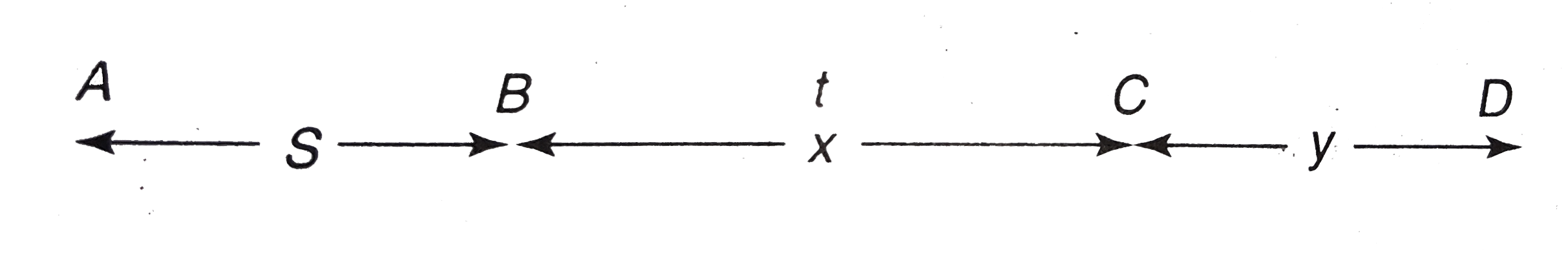Question

A car , starting from rest, accelerates at the rate `f` through a distance `S` then continues at constant speed for time `t` and then decelerates at the rate `(f)/(2)` to come to rest . If the total distance traversed is `15 S` , then
A. `S = (1)/(2) ft^2`
B. `S = (1)/(4) ft^2`
C. `S = (1)/(72) ft^2`
D. `S = (1)/(6) ft^2`

Answer 1

Correct Answer - C
Let car starts from point `A` from rest and moves up to point `B` with acceleration `f`.
Velocity of car at point `B`, `v = sqrt(2 f S)`
`[As v^2 = u^2 + 2 as]`
Car moves distance `BC` with this constant velocity in time `t`.
`x = sqrt(2 f S) . t` ...(i) `[As s = ut]`
So the velocity of car at point `C` also will be `sqrt(2 fs)` and finally car stops after covering distance `y`.
Distance `CD` i.e., `y = ((sqrt(2 f S))^2)/(2(f//2)) = (2 fs)/(f) = 2 S` ...(ii)
`[AS v^2 = u^2 - 2 as rArr s = u^2//2 a]`
So, total distance `AD = AB + BC + CD= 15 S` (given)
`rArr S + x + 2 S = 15 S rArr x = 12 S`
Substituting the value of `x` in equation (i) we get
`x = sqrt(2 f S).t rArr 12 S = sqrt(2 f S) . t`
`rArr 144 S^2 = 2 f S.t^2`
`rArr S = (1)/(72) ft^2`.