Question

A ball moving with a speed of `9m//s` strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of `30^(@)` with the original line of motion. Find the speeds of the two balls after collision.

Answer 1

Correct Answer - A
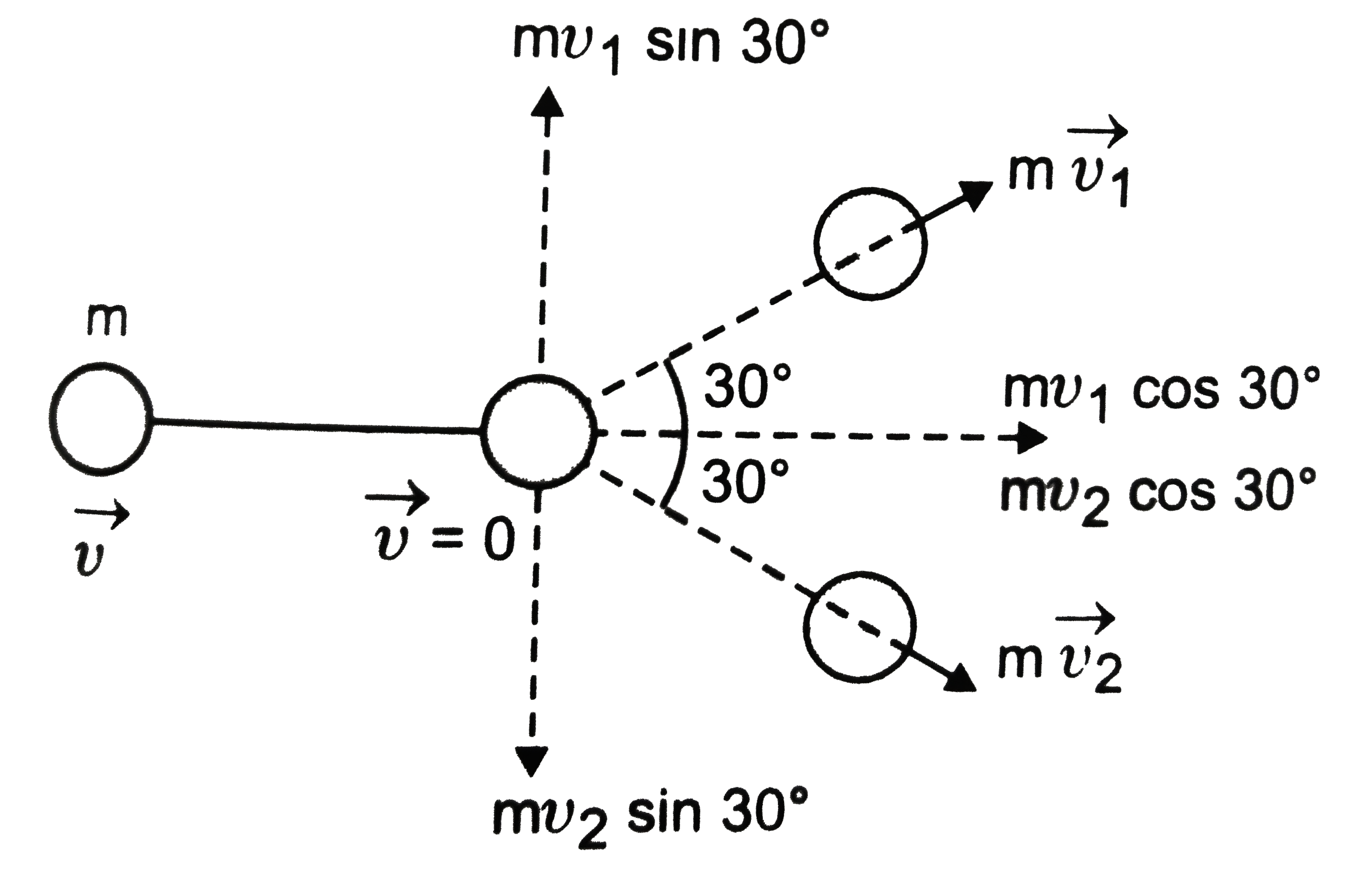
As shown in figure.
application of the law of conservation of linear momentum perpendicular to intial line of motion, gives
`0=m upsilon_(1) sin 30^(@)- m upsilon^(2) sin 30 ^(@) :. upsilon_(1)=upsilon _(2)`
Applying the same principle along the line of motion,
`mxxupsilon+mxx0=2 m upsilon_(1) cos 30^(@)+m upsilon_(2) cos 30^(@)`
`mxx6+mxx0=2 m upsilon_(1) cos 30^(@)=2 m upsilon_(1)(sqrt(3))/(2)`
`upsilon_(1)=(6)/(sqrt(3))=2 sqrt(3) m//s`