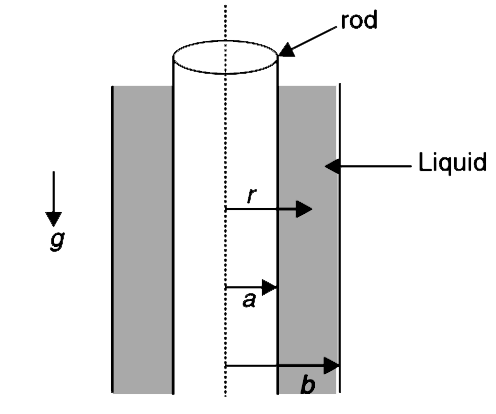
A vertical steel rod has radius a. The rod has a coat of a liquid film on it. The liquid slides under gravity. It was found that the speed of liquid layer at radius r is given by
`v=(rhogb^(2))/(2eta)ln((r)/(a))-(rhog)/(4eta)(r^(2)-a^(2))`
Where b is the outer radius of liquid film, `eta` is coefficient of viscosity and `rho` is density of the liquid.
(i) Calculate the force on unit length of the rod due to the viscous liquid?
(ii) Set up the integral to calculate the volume flow rate of the liquid down the rod. [you may not evaluate the integral]