Question

An object `A` is kept fixed at the point ` x= 3 m` and `y = 1.25 m` on a plank `p` raised above the ground . At time ` t = 0 ` the plank starts moving along the `+x` direction with an acceleration ` 1.5 m//s^(2) `. At the same instant a stone is projected from the origin with a velocity `vec(u)` as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle ` 45(@)` to the horizontal . All the motions are in the ` X -Y `plane . Find ` vec(u)` and the time after which the stone hits the object . Take ` g = 10 m//s`

Answer 1

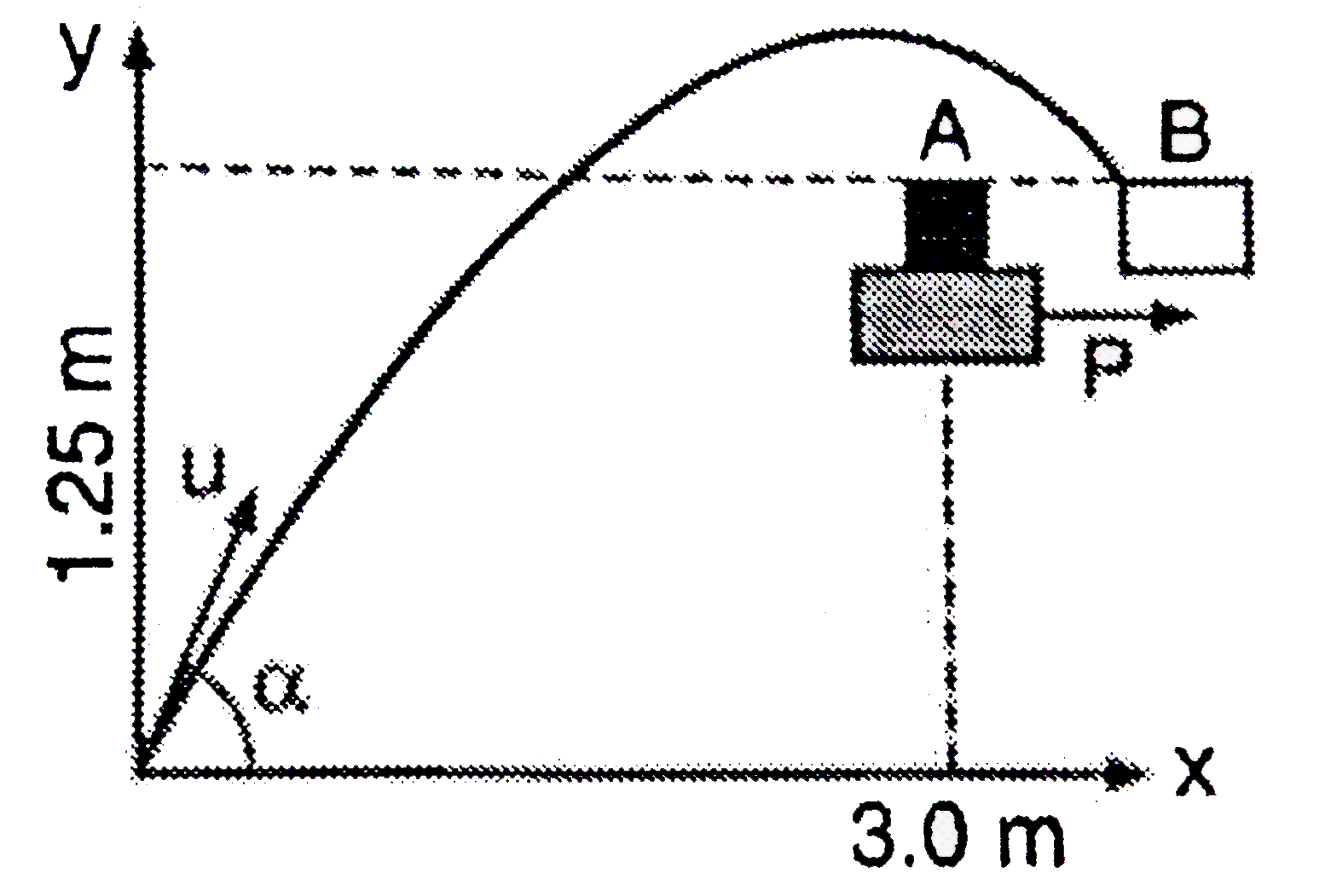
Let the projectile be projected with velocity u at an angle `alpha` with horizontal. As the projectile hits the object B after time t, where its velocity is at `45^(@)` to horizontal during downward motion, so,
`(u sin alpha-gt)/(u cos alpha)=-1`
`therefore u cos alpha+ u sin alpha=gt` ........(i)
Further, `3+(1)/(2)xx1.5t^(2)=u cos alpha-t` .........(ii)
and `1.25=u sin alpha.t-(1)/(2)g t^(2)` ..........(iii)
From Eqn. (i), `u sin alpha.t=g t^(2)-ucos alpha.t`
Substituting for `u cos alpha.t` from Eqn. (ii),
`u sin alpha.t=g t^(2)-(3+(1)/(2)xx1.5t^(2))`
`=10t^(2)-3-0.75t^(2)`
From Eqn. (iii), 1.25`+5t^(2)=10t^(2)-3-0.75t^(2)`
i.e., 4.25`t^(2)=4.25` or t=1 s, ignoring negative value of t.
From Eqns. (ii) and (i),
`u cos alpha=3+0.75=3.75`
and `u sin alpha=10xx1=-3.75=6.25`
Squaring and adding.
`u=sqrt((3.75)^(2)+(6.25)^(2))=7.3m//s`
and dividing, `tan alpha=(6.25)/(3.75)=(5)/(3)`
`therefore alpha=tan^(-1)(5//3)=59^(@)`