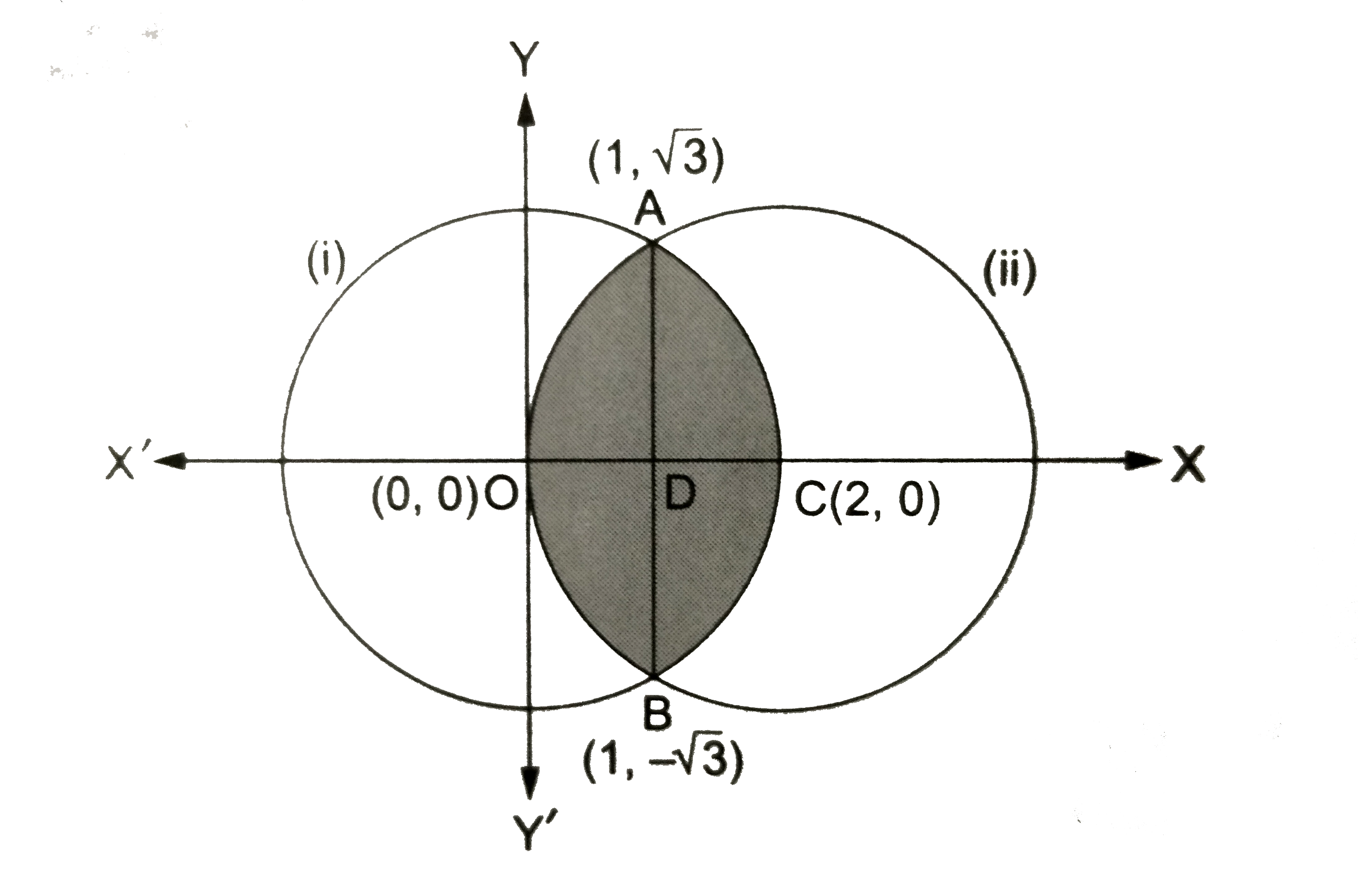
`x^2+y^2=4` is a circle with its centre at O(0,0) and radius = 2 units And , `(x-2)^2=4` is a circle with is centre at C(2,0) and radius 2 units
The given circles are
`x^2 +y^2)=4` is a circle with its centre at C(2,0) and radius = 2 units.
The given cirlcles are
`x^2 +Y^2=4`
and `(x-2)^2=4`
Eliminating y form (i) and (ii) we get
`4-x^2=4-(x-2)^2rArr 4x = 4 rArr x = 1 `
Putting `x=1 in (i),we get y^2= 3 rArr y = pm sqrt(3)`
Thus the points of intersection of the two circles are `A (1,3sqrt(3))` and `B(1,-sqrt(3))`
Both the circles are symmetrical about the x-axis.
Required area `=2 "area"(AOCA)`
`2("area AODA + area CADC")`
`2underset(0)overset(1)int " y dx for circle (ii)"+2underset(1)overset(2)int"y dx for circle (i)"`
`2underset(0)overset(1)intsqrt(4-(x-2)^2)dx +2 underset(1)overset(2)intsqrt(4-x^2)dx`
`=[((x-2)sqrt(4-(x-2)^2))/(2)=4/2sin^(-1)""(x-2)/2]_(-0)^1+[(xsqrt(4-x^2))/(2)+4/2.sin^(-1)""x/2]_1^0`
`=2[{(-sqrt(3)/(2)+2sin^(-1)""((-1)/2)}-{0+2 sin^(-1)(-1)}+{2sin^(-1)(1)-(sqrt(3))/2-2sin^(-1)(1/2)}]`
`={(-sqrt3)/2+2(pi/2)-2((-pi)/2)+(2.pi/2-sqrt(3)/2-2xxpi/6)}`
`=2((4pi)/3-sqrt(3))`sq units
Hence , the required area is `2((4pi)/3-sqrt(3))`sq units
