Question

A thin flexible wire of length `L` is connected to two adjacent fixed points carries a current `I` in the clockwise direction, as shown in the figure.When system is put in a uniform magnetic field of strength `B` going into the plane of paper, the wire takes the shape of a circle.The tension in the wire is:

A. `IBL`
B. `(IBL)/(pi)`
C. `(IBL)/(2pi)`
D. `(IBL)/(4 pi)`

Answer 1

Correct Answer - C
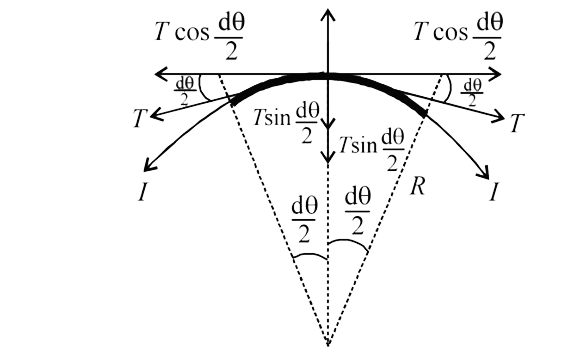
Let us consider an elemental length ` dl ` subtending an angle ` d theta` at the centre of the circle. Let ` F_(B) be the3 magnetic force acting on this length . Then
`F_(B) = BI(dl) ` directed upwards as shown
` = BI(Rd theta)` ` { because angle(d theta = (arc(dl))/(radius R)]` lt brgt ` = (BI(L))/(2 pi) d theta ` `[ because 2 pi R = L rArr R = (L)/(2 pi)]`
Let ` T` be the tension in the wire acting along both ends of the elemental length as shown . On resolving ` T` , we find that the components. ` T cos ((d theta)/(2))` cancel out and the components . ` T sin ((d theta)/(2))` add up to balance `F_(B)`.
At equilibrium ` 2 T sin ((d theta)/(2)) = BI (L)/(2 pi) d theta`
rArr ` 2 T(d theta)/(2) = BI(L)/(2 pi) d theta ` [ because (d theta )/(2) = small ]`
rArr = (BIL)/(2 pi)`