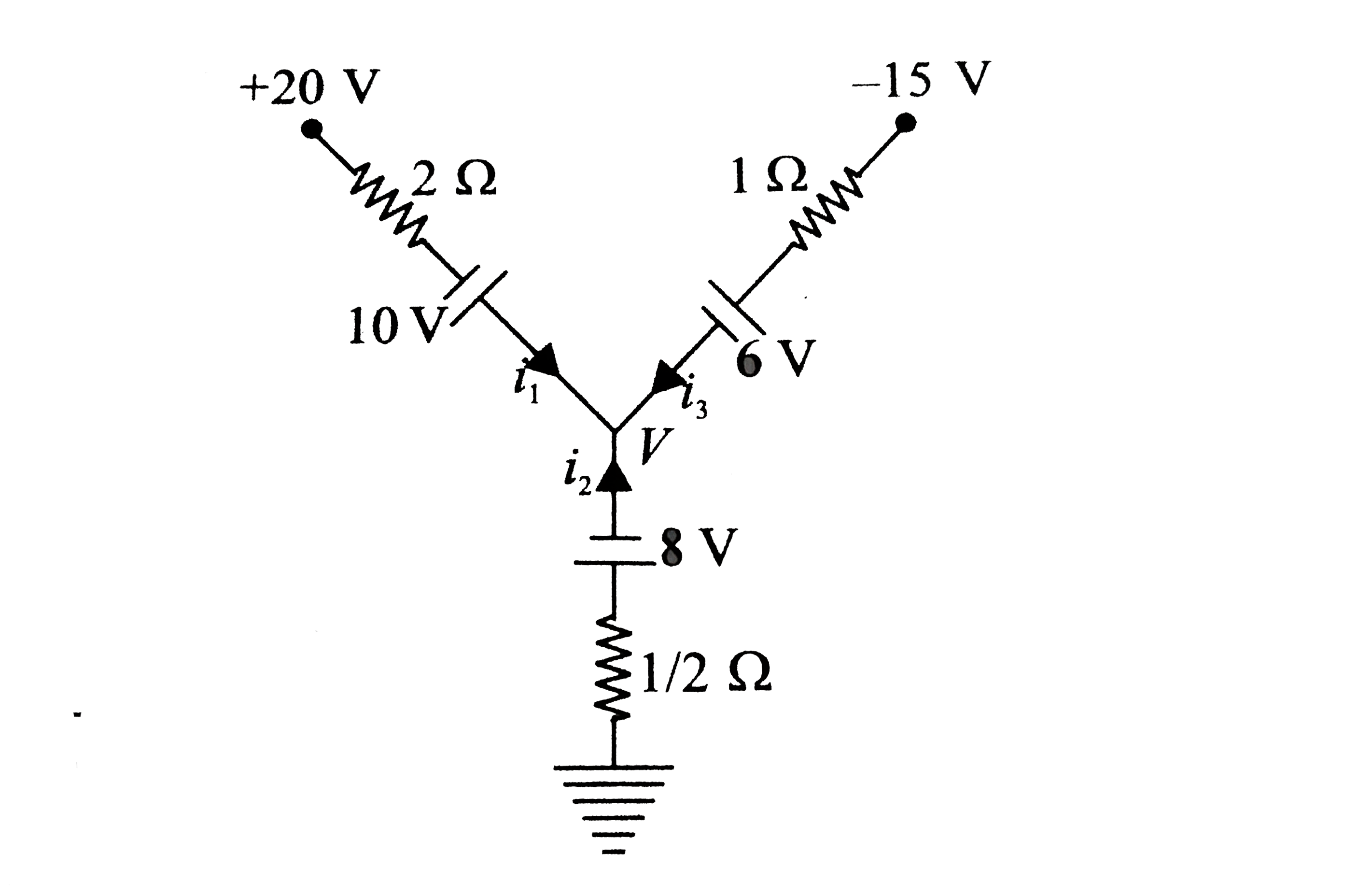Question

in the network of three cells, find the potential V of their funcion.

Answer 1

Applying KCL for the individual branches, we get
`20 - i_1(2) +10 = V (i)`
`0 - i_2((1)/(2)) - 8 =V (ii)`
`-15 - i_3(1) -6 =V (iii)`
`ik_1 +i_2+i_3 = 0 (iv)`
Putting `i_1, i_2, and i_3` from Eqs. (i),
(ii) and (iii) in Eq. (iv). we have
`(30 -V)/(2) +(V+8)/( - 1//2) +(V +21)/(-1) = 0`
or ` V = -(44)/(7)V`