Question

A convex lens of focal length 20 cm is cut long its diameter and the two halves are displaced by `t = 1` cm along the principal axix. A monochromatic point source of wavelength 476 nm is placed at a distance 40 cm from the first half, as shown in Fig. 2.21. Find the position of the first maximum.

Answer 1

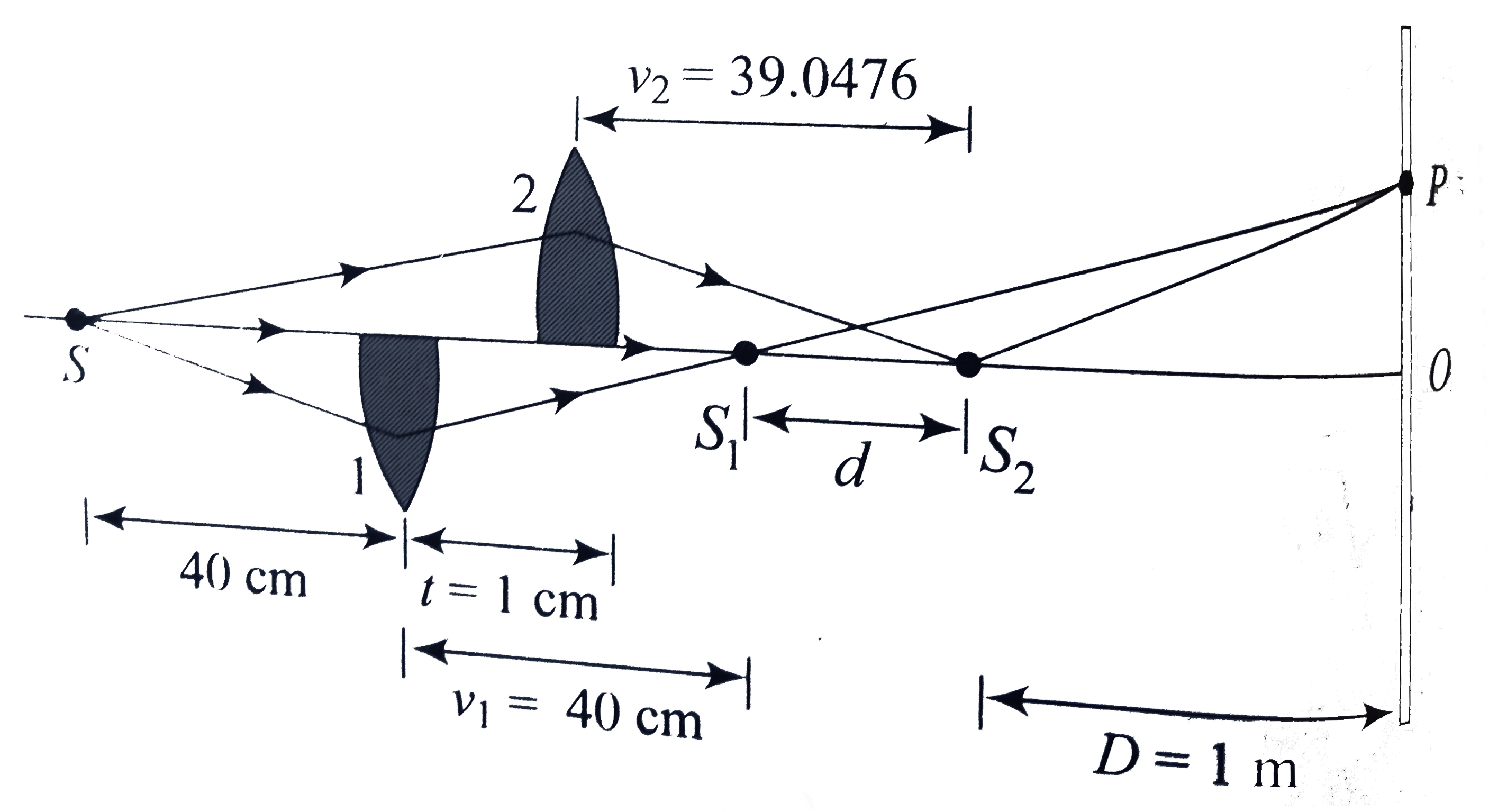
Using the formula
`nu = (fu_(1))/(u_(1) - f) = ((20)(40))/((40 - 20)) = 40 cm`
and `nu = (u_(2) f)/(u_(2) - f) = ((41)(20))/(41 - 20) = 39.0476 cm`
`d = nu_(2) - nu_(1) = 0.0476 cm = 0.476 mm`
The optical path difference at P is
`Delta x_(p) = (SS_(2) + S_(1) P) = S_(1) S_(2) + S_(2) P - S_(1) P`
`= (SS_(2) + S_(2) P) - (SS_(1) +S_(1) P)`
`= (SS_(2) - SS_(1)) - (S_(1) P - S_(2) P)`
` = d - (S_(1) P - S_(2) P)`
We know that
`S_(1) P - S_(2) P = d [1 - (y^(2))/(2D^(2))]`
`Delta x_p = d - d [1 - (y^(2))/(2D^(2))] = (y^(2) d)/(2D^(2))`
The position of hte n th maximumis given by
`(Y^(2) d)/(2D^(2)) = n lambda or y = D sqrt((2n lambda)/(d)`
The Position of the first maximum is given by
`y = 10^(3) sqrt((2(1)(0.476 xx 10^(-3)))/(0.476)) = 44.72 mm`