Question

If Rolle’s theorem holds for the function f(x) = x³ + px² + qx + 5, x ∈ [1, 3] with c = 2 + 1/√3, find the values of p and q.

Answer 1

The Rolle’s theorem holds for the function f(x)

Also, there exists at least one point c ∈ (1, 3) such that f'(c) = 0.

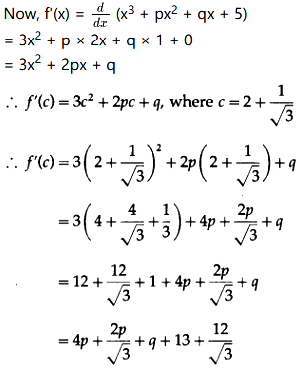
But f'(c) = 0

Multiplying equation (1) by √3, we get

4√3p + √3q= -13√3

Subtracting this equation from (2), we get

2p = -12 ⇒ p= -6 

∴ from (1), 4(-6) + q = -13 ⇒ q = 11

Hence, p = -6 and q = 11.