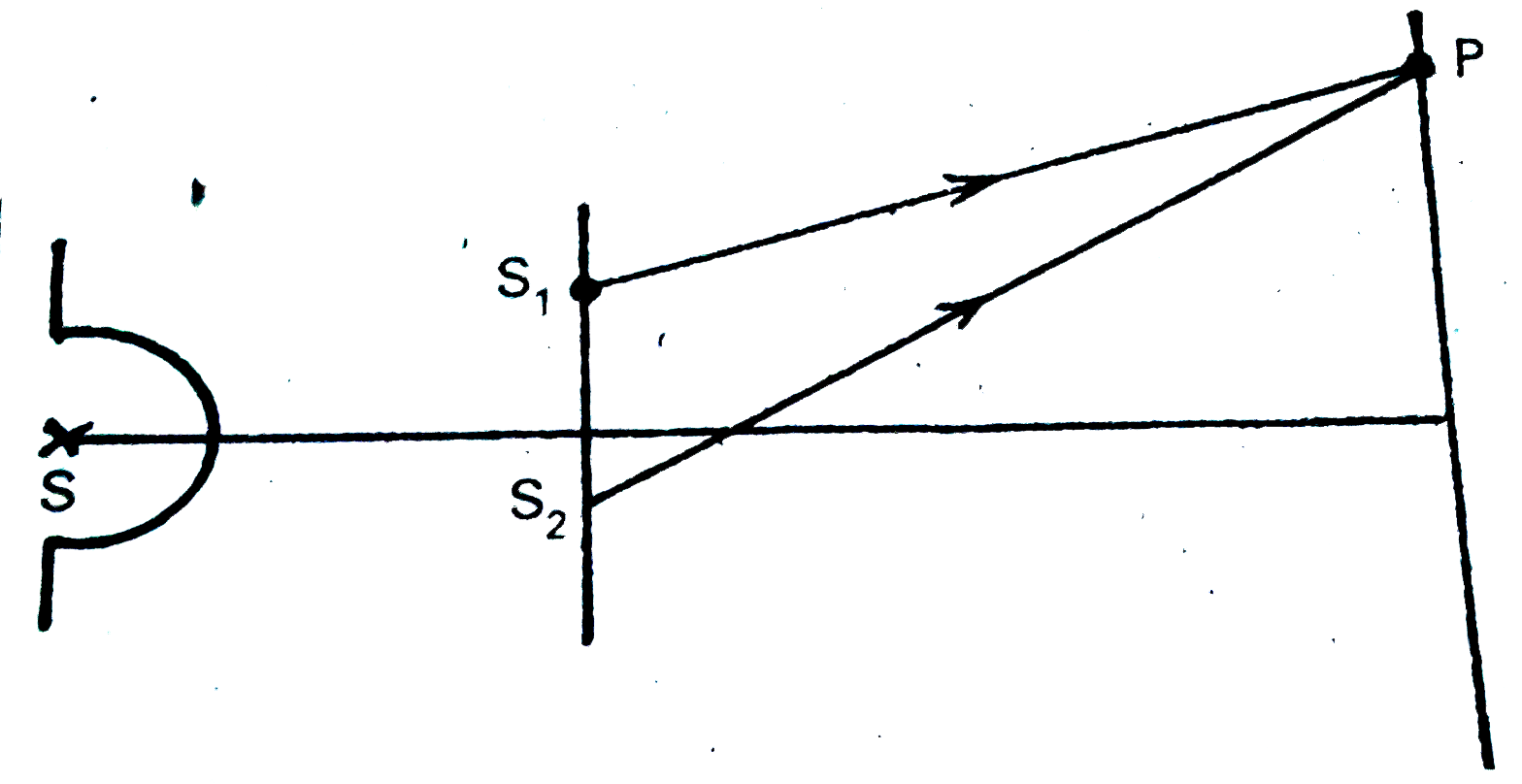
Let `y_(1) and y_(2)` be the displacements of the two waves having same amplitude a and `phi` is the phase difference between them.
`y_(1) =a sin omegt....(1)`
`y_(2)=a sin (omegat+phi)....(2)`
The resultant displacement `y=y_(1)+y_(2)`
`y=a sin omegat+a sin (omegat+phi)`
`y=a sin omegat+a sin omegat cos phi+a cos omegat sin phi`
`y=a sin omegat [1+cos phi]+cos omegat (a sin phi)`....(3)
Let `R cos theta=a(1+cos phi).....(4)`
`R sin phi=a sin phi ....(5)`
`y=R sin omegat. cos theta+R cos omegat, sin omega`
`y=R sin (omegat+theta).....(6)`
where R is the resultant amplitude at P, squaring equations (4) and (5), then adding `R^(2)[cos^(2) theta+sin^(2) theta]=a^(2) phi+2 cos phi+sin^(2)phi]`
`R^(2)[1]=a^(2)[1+1+2 cos phi]`
`I=R^(2)=2a^(2)[1+cos phi]=2a^(2)xx2cos^(2) (phi)/(2), I=4a^(2) cos^(2) (phi)/(2)` ......(7)
(i) Minimum intensity `(I_(max))`
`cos^(2) (phi)/(2)=1`
`phi=2npi, "Where "n=0,1,2,3,......`
`phi=0,2pi,4pi,6pi`
`therefore I_(max)=4a^(2)`
(ii) Minimum intensity `(I_(min))`
`cos^(2) (theta)/(2)=0`
`phi=(2n+1)pi" where "n=0,1,2,3,......`
`phi=pi,3pi,5pi,7pi......`
`I_(min)=0`.