Question

If BL and CM are the medians of a triangle ABC right angled at A, then the value of 4(BL² + CM²) =

(A) 3BC²

(B) 5BC²

(C) 7BC²

(D) BC²

Answer 1

Correct option is (B) 5BC²

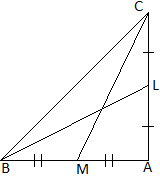
\(\because\) BL is median

\(\therefore\) \(AL=CL=\frac{AC}2\)

& CM is median

\(\therefore\) \(AM=BM=\frac{AB}2\)

By applying Pythagoras theorem in right \(\triangle BAC,\) we get

\(BC^2=AB^2+AC^2\)    ____________(1)

By applying Pythagoras theorem in right \(\triangle MAC,\) we get

\(CM^2=AC^2+AM^2\)  ____________(2)

By applying Pythagoras theorem in right \(\triangle BAL,\) we get

\(BL^2=AB^2+AL^2\)    ____________(3)

By adding (1) & (2), we get

\(BL^2+CM^2=AB^2+AC^2+AL^2+AM^2\)

\(=AB^2+AC^2+(\frac{AC}2)^2+(\frac{AB}2)^2\)     \((\because AM=\frac{AB}2\;\&\;AL=\frac{AC}2)\)

\(=AB^2+AC^2+\frac14(AB^2+AC^2)\)

\(=BC^2+\frac14BC^2\)           (From (1))

\(=\frac54BC^2\)

\(\therefore\) \(4(BL^2 + CM^2) =\) \(5BC^2\)

Answer 2

Correct option is: (B) 5BC²