Correct option is (A) XY/XZ = YP/PZ
The interior angle bisector theorem states that the angle bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
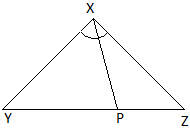
Given : A \(\triangle XYZ \) in which XP is the internal bisector of \(\angle X\) and meets YZ at P.
\(\therefore\) \(\frac{YP}{PZ}=\frac{XY}{XZ}\) (By internal bisector theorem)
\(\Rightarrow\) \(\frac{XY}{XZ} = \frac{YP}{PZ}\)