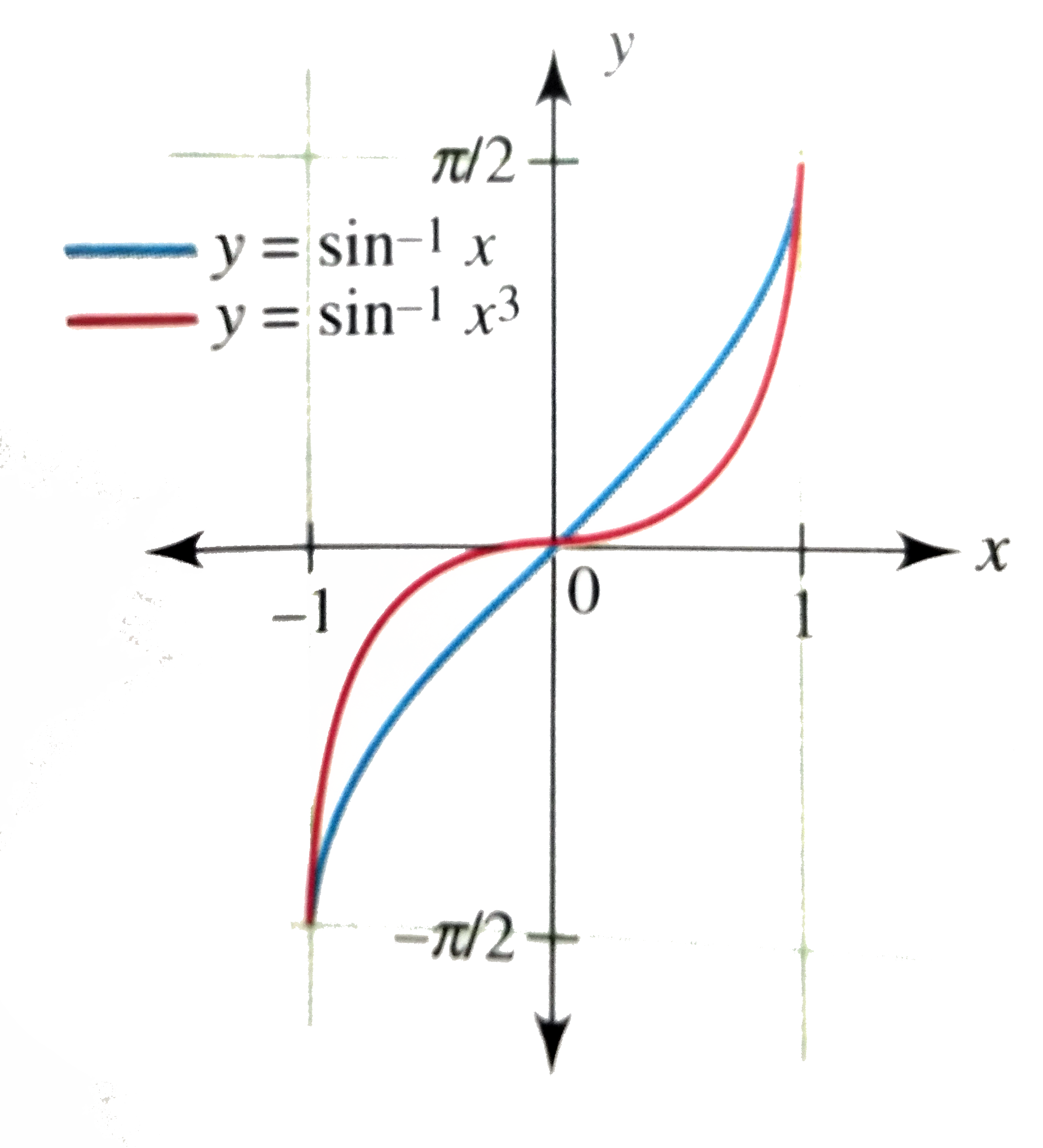
We have `y = f(x)= sin^(-1)x^(3)`
We must have`-1lex^(3)le1therefore-1lexle1`
Also `sin^(-1)x^(3)" is increasing as "sin^(-1)" x and x"^(3)" both are increasing"`
`f(-1)=sin^(-1)(-1)^(3)=sin^(-1)(-1)=-pi//2`
`f(-1)=sin^(-1)(-1)^(3)=sin^(-1)(-1)=pi//2`
`f(0)=sin^(-1)0=0`
`f(1)=sin^(-1)=pi//2`
For `-1lexlt0,xltx^(3)thereforesin^(-1)xltsin^(-1)x^(3)" heance the graph of "y=sin^(-1)x^(3)" lies below the graph of "y = sin^(-1)x`.
For `-1lexlt0,xltx^(3)thereforesin^(-1)xltsin^(-1)x^(3)" heance the graph of "y=sin^(-1)x^(3)" lies above the graph of "y = sin^(-1)x`.
Therefore graph of both functions ar as shown in the followin figure.