Question

Draw the graph of `[y] = cos x, x in [0, 2pi],` where `[*]` denotes the greatest integer function.

Answer 1

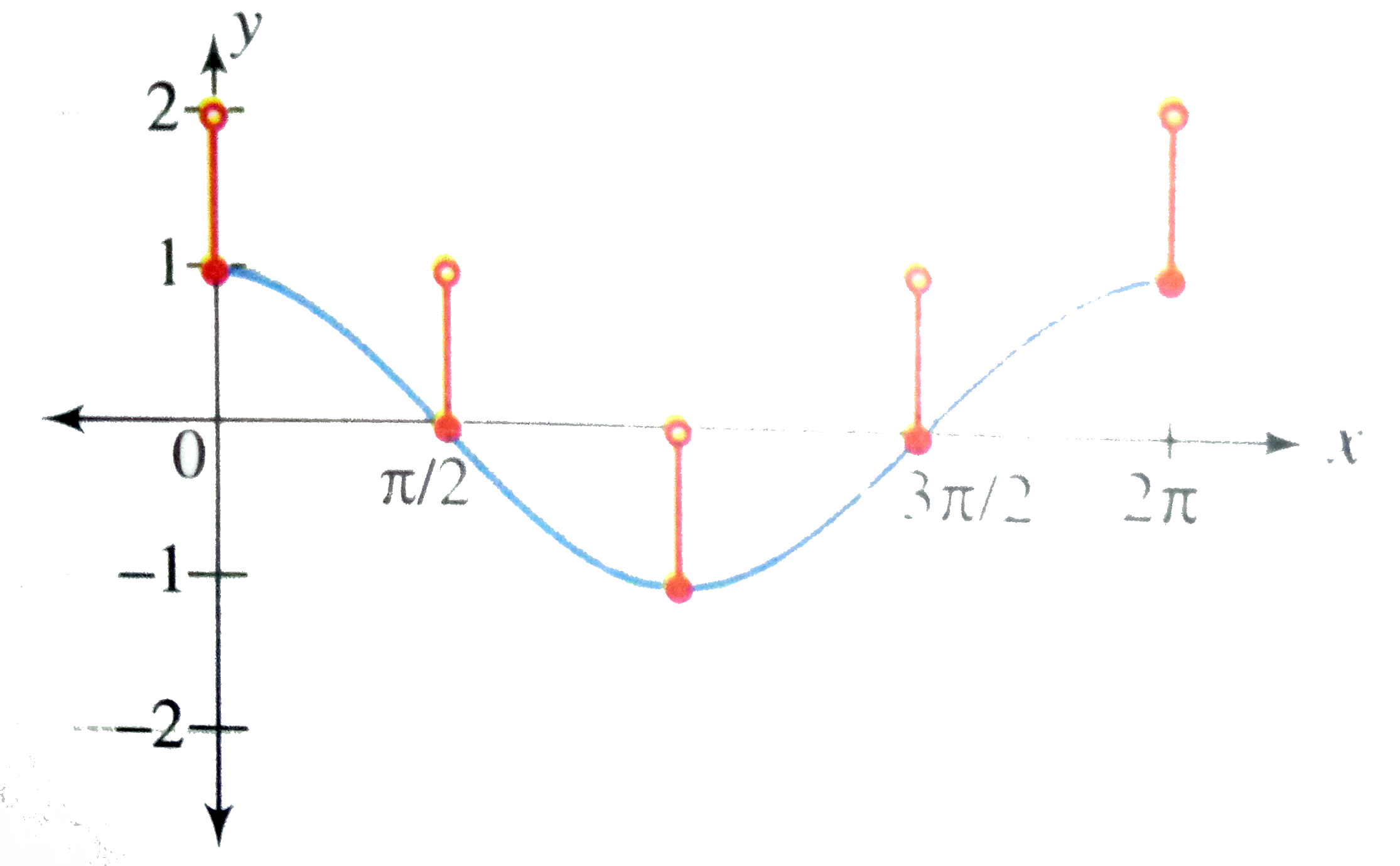
We have [y] = cos x
This is satisfied for the integral values of cos x.
`therefore` cos x = -1, 0, 1
When `cos x = -1, x = (2n + 1) (pi)/(2), n in Z`
And `[y] = -1 therefore -1 le y lt 0`
When `cos x = 1, x = 2npi, n in Z`
And `[y] = 1 therefore 1 le y lt 2`
when `cos x = 0, x = (2n + 1) (pi)/(2), n in Z`
And `[y] = 0 therefore 0 le y lt 1`
Hence, graph of the function is as shown in the following figure.