Question

discuss rolling on inclined plane and arrive at the expression for the acceleration.

Answer 1

                * A round object of mass (m) and radius (R) is rolling down on inclined plane without slipping.

               * There are two force acting on the object along the inclined plane.

               * One is the component of gravitational force (mg sinΦ) and the other is the static friction force (f).

               * The other component of gravitational force (mg cosΦ) is cancelled by the normal force (N)  exerted by the plane. 

               * The free body diagram (FBD)  of the object. 

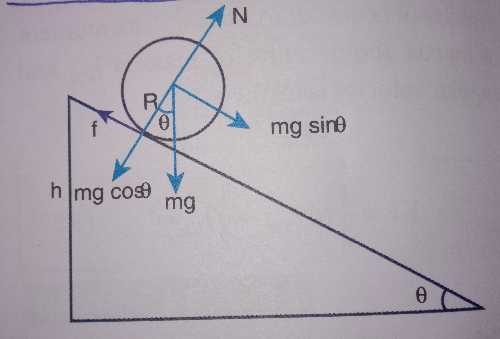
mg sinΦ is the supporting force and f is the opposite force.

            mg sinΦ-f=ma...(1)

The mg sinΦ cannot torque as it passes through it but the frictional force f can set torque of Rf

            Rf=Iα

By using the relation a=rα,and moment of inertia I=mk²,we get

            Rf=mk²a/R;

            f=ma[k²/R^2]

Now equ (1) becomes

              mg sinΦ=ma[K^2/R2]=ma

              mg sinΦ=ma+ma[k²/M^2]

                 a[1+K²/R²]=g sinΦ

After rewriting it for acceleration we ge

             a=gsinΦ/[1+K²/R²]