Question

Explain gauge pressure and absolute pressure within a liquid open to the atmosphere. 

OR 

Explain the effect of gravity on fluid pressure

Answer 1

Consider a cylindrical fluid column of uniform density ρ, area of cross section A and height h,

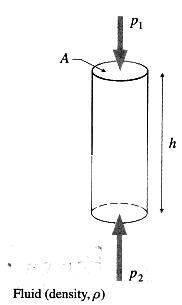
The mass of the fluid within the column is m = density × volume 

= ρAh

If p₁ and p₂ are the pressures at the top and bottom faces of the column, the forces on the top and bottom faces are respectively. 

F₁ = p₁A + mg (downward) and F₂ = p₂A (upward) If the column is in equilibrium,

F₂ = F₁ 

∴ p₂A = p₁A + mg = p₁A + ρAhg 

∴ P₂ ~ P₁  = ρhg

If p₁ = p₀ = atmospheric pressure, the gauge pressure 

P₂ – p₀ = ρhg

In the absence of gravity, P₂ = p₀ But since atmospheric pressure is equal to the weight per unit area of the entire air column above, even p0 will be zero in the absence of gravity.

Answer 2

Qualitatively, gauge pressure is the pressure due to the weight of the fluid solely, meaning without the atmospheric pressure being considered. In contrast, absolute pressure is the total pressure considering both pressures: the one due to the weight of the fluid, and the pressure due to the atmosphere (atmospheric pressure).

hope this helps.