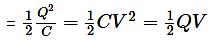Question

Show that the energy of a charged capacitor is 1/2 CV² . Also, express this in other forms.

OR 

Derive an expression for the energy stored in a charged capacitor. Express it in different forms.

Answer 1

To charge a capacitor, an external agent has to do work against the electrostatic forces due to the charges already present on the plates of the capacitor.

Let C be the capacitance of the capacitor. Let Q and V be the final charge and the potential difference respectively when the capacitor is charged. Let q be the charge on the capacitor at some stage during the charging and v, the corresponding potential difference between the plates. The work done by an external agent in bringing additional small charge dq from infinity and depositing it on the capacitor is

dW = potential difference × charge = v dq 

But C = \(\cfrac qv\)

\(\therefore\) dW = \(\cfrac qC\)dq

The total work done in charging the capacitor is

This work is stored in the form of potential energy, in the electric field in the medium between the plates of the capacitor.

∴ Energy of a charged capacitor