NCERT Solutions Class 10 Maths Chapter 13 Surface Areas and Volumes

Question

Our NCERT Solutions Class 10 Maths Chapter 13 Surface Areas and Volumes is one of the best ways to study for the CBSE term II examination. We have discussed all kinds of concepts and topics in such a way that it is easy to understand for the students. NCERT solutions provided here are based on the latest syllabus proposed by the CBSE. Students who are looking to clear the basic concepts of NCERT chapters must or preparing for competitive exams like JEE Mains, JEE Advance, NTSE, Olympiad, or any similar exams must opt for our solutions.

NCERT Solutions Class 10 Maths students get to learn about all kinds of different topics in a very effective way. The chapter on mensuration is one such topic. In this chapter on Surface Area and Volumes, we will learn to find the area and volume of a 3D figure like area of

• Cube:
  • area = 6a² 
  • volume = a³
• Cone:
  • Volume = (1/3)πr²h
  • Slant height of a cone = √(r² + h²)
  • Lateral surface area of a cone = \(\pi\)rs = \(\pi\)r√(r² + h²)
  • Base area of a cone(circle) = πr²
  • Total surface area of cone =  L + B = \(\pi\)rs + \(\pi\)r² = \(\pi\)r(s + r) = \(\pi\)r(r + √(r² + h²))
• Cylinder:
  • Volume: \(\pi\)r² h
  • Surface area: 2\(\pi\)r h + 2\(\pi\)r²
• Cuboid:
  • Volume: l∙b∙h
  • Surface area of cuboid: 2(l∙b+b∙h+h∙l), where ‘l’ is length, ‘b’ is the breadth and ‘h’ is height.
• Sphere:
  • Volume: 4/3 \(\pi\)r³
  • Surface area = 4 \(\pi\)r²
• Hemisphere:
  • Volume: (2/3)\(\pi\)r³
  • Surface area: 3\(\pi\)r²
• Surface Area of a combination of solids
• Volume of a combination of solids
• Conversion of solids from one 3D figure to another 3D figure.
• Frustum of a cone.

We have provided NCERT Solutions Class 10 Maths will give an overall understanding of all kinds of topics. One must go through our topics to gain clarity and expertise in the subject matter.

All solutions at your fingertip get started now.

Answer 1

NCERT Solutions Class 10 Maths Chapter 13 Surface Areas and Volumes

1. 2 cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboids.

Answer:

Given that, 

Volume of cubes = 64 cm³ 

(Edge)³ = 64 

Edge = 4 cm

If cubes are joined end to end, the dimensions of the resulting cuboid will be 4 cm, 4 cm, 8 cm.

\(\therefore\) Surface area of cuboids = 2(lb + bh + lh)

2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel. [Use \(\pi\) = 22/7]

Answer:

It can be observed that radius (r) of the cylindrical part and the hemispherical part is the same (i.e., 7 cm). 

Height of hemispherical part = Radius = 7 cm 

Height of cylindrical part (h) = 13 −7 = 6 cm 

Inner surface area of the vessel = CSA of cylindrical part + CSA of hemispherical part

= 2\(\pi\)rh + 2\(\pi\)r²

Inner surface area of vessel 

3. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy. [Use \(\pi\) = 22/7]

Answer:

It can be observed that the radius of the conical part and the hemispherical part is same (i.e., 3.5 cm). 

Height of hemispherical part = Radius (r) = 3.5 = 7/2 cm 

Height of conical part (h) = 15.5 −3.5 = 12 cm

Slant height (l) of conical part = \(\sqrt{r^2 + h^2}\)

Total surface area of toy = CSA of conical part + CSA of hemispherical part

4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid. [Use \(\pi\) = 22/7]

Answer:

From the figure, it can be observed that the greatest diameter possible for such hemisphere is equal to the cube’s edge, i.e., 7cm. 

Radius (r) of hemispherical part = 7/2 = 3.5cm 

Total surface area of solid = Surface area of cubical part + CSA of hemispherical part − Area of base of hemispherical part

= 6 (Edge)² + 2\(\pi\)r² - \(\pi\)r²

= 6 (Edge)² + \(\pi\)r² 

Total surface area of solid = 6(7)² + \(\frac{22}{7}\times\frac{7}{2}\times\frac{7}{2}\)

= 294 + 38.5

= 332.5 cm²

5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.

Answer:

Diameter of hemisphere = Edge of cube = l 

Radius of hemisphere = l/2 

Total surface area of solid = Surface area of cubical part + CSA of hemispherical part − Area of base of hemispherical part

= 6 (Edge)² + 2\(\pi\)r² - \(\pi\)r²

= 6 (Edge)² + \(\pi\)r² 

Total surface area of solid

6. A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use \(\pi\) = 22/7]

Answer:

It can be observed that 

Radius (r) of cylindrical part = Radius (r) of hemispherical part

= \(\frac{Diameter \,of \,the \,capsule}{2}\)

= \(\frac{5}{2}\) 

Length of cylindrical part (h) = Length of the entire capsule − 2 × r 

= 14 − 5 

= 9 cm 

Surface area of capsule = 2×CSA of hemispherical part + CSA of cylindrical part

7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m² . (Note that the base of the tent will not be covered with canvas.)  [Use \(\pi\) = 22/7]

Answer:

Given that, 

Height (h) of the cylindrical part = 2.1 m 

Diameter of the cylindrical part = 4 m 

Radius of the cylindrical part = 2 m 

Slant height (l) of conical part = 2.8 m 

Area of canvas used = CSA of conical part + CSA of cylindrical part

Cost of 1 m² canvas = Rs 500 

Cost of 44 m² canvas = 44 × 500 = 22000

Therefore, it will cost Rs 22000 for making such a tent.

Answer 2

 8. From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm².   [Use \(\pi\) = 22/7]

Answer:

Given that, 

Height (h) of the conical part = Height (h) of the cylindrical part = 2.4 cm 

Diameter of the cylindrical part = 1.4 cm 

Therefore, radius (r) of the cylindrical part = 0.7 cm

Slant height (l) of conical part = \(\sqrt{r^2 + h^2}\)

Total surface area of the remaining solid will be = CSA of cylindrical part + CSA of conical part + Area of cylindrical base

The total surface area of the remaining solid to the nearest cm² is 18 cm².

 9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in given figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.   [Use \(\pi\) = 22/7]

Answer:

Given that, 

Radius (r) of cylindrical part = Radius (r) of hemispherical part = 3.5 cm 

Height of cylindrical part (h) = 10 cm 

Surface area of article = CSA of cylindrical part + 2 × CSA of hemispherical part

10. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.

Answer:

Given that, 

Height (h) of conical part = Radius(r) of conical part = 1 cm 

Radius(r) of hemispherical part = Radius of conical part (r) = 1 cm 

Volume of solid = Volume of conical part + Volume of hemispherical part

11. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. if each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)  [Use \(\pi\) = 22/7]

Answer:

From the figure, it can be observed that 

Height (h₁) of each conical part = 2 cm 

Height (h₂) of cylindrical part = 12 − 2 × Height of conical part 

= 12 − 2 ×2 = 8 cm 

Radius (r) of cylindrical part = Radius of conical part = 3/2 cm 

Volume of air present in the model = Volume of cylinder + 2 × Volume of cones

12. A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see the given figure).  [Use \(\pi\) = 22/7]

Answer:

It can be observed that 

Radius (r) of cylindrical part = Radius (r) of hemispherical part = \(\frac{2.8}{2}\) = 1.4 cm

Length of each hemispherical part = Radius of hemispherical part = 1.4 cm 

Length (h) of cylindrical part = 5 − 2 × Length of hemispherical part = 5 − 2 × 1.4 = 2.2 cm 

Volume of one gulab jamun = Vol. of cylindrical part + 2 × Vol. of hemispherical part

Volume of 45 gulab jamuns = 45×25.05 = 1,127.25 cm³ 

Volume of sugar syrup = 30% of volume

13. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboids are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see the following figure). [Use \(\pi\) = 22/7]

Answer:

Depth (h) of each conical depression = 1.4 cm

Radius (r) of each conical depression = 0.5 cm 

Volume of wood = Volume of cuboid − 4 × Volume of cones

14. A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.

Answer:

Height (h) of conical vessel = 8 cm 

Radius (r₁) of conical vessel = 5 cm 

Radius (r₂) of lead shots = 0.5 cm Let n number of lead shots were dropped in the vessel. 

Volume of water spilled = Volume of dropped lead shots

Hence, the number of lead shots dropped in the vessel is 100.

15. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass. [Use π = 3.14]

Answer:

From the figure, it can be observed that 

Height (h₁) of larger cylinder = 220 cm 

Radius (r₁) of larger cylinder = 24/2 = 12 cm 

Height (h₂) of smaller cylinder = 60 cm 

Radius (r₂) of smaller cylinder = 8 cm

Total volume of pole = Volume of larger cylinder + Volume of Smaller cylinder

Mass of 1 cm³ iron = 8g 

Mass of 111532.8 cm³ 

= 111532.8×8g 

= 892262.4g 

= 892.262 Kg

Answer 3

16. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.  [Use \(\pi\) = 22/7]

Answer:

Radius (r) of hemispherical part = Radius (r) of conical part = 60 cm 

Height (h₂) of conical part of solid = 120 cm 

Height (h₁) of cylinder = 180 cm 

Radius (r) of cylinder = 60 cm 

Volume of water left = Volume of cylinder − Volume of solid

= Volume of cylinder - (Volume of cone + Volume of hemisphere)

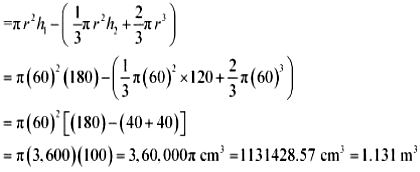
17. A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter o the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3 . Check whether she is correct, taking the above as the inside measurements, and π = 3.14.

Answer:

Height (h) of cylindrical part = 8 cm 

Radius (r₂) of cylindrical part = 1 cm 

Radius (r₁) spherical part = 4.25 cm 

Volume of vessel = Volume of sphere + Volume of cylinder

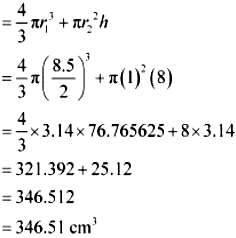
Hence, she is wrong.

18. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.

Answer:

Radius (r₁) of hemisphere = 4.2 cm 

Radius (r₂) of cylinder = 6 cm 

Let the height of the cylinder be h. 

The object formed by recasting the hemisphere will be the same in volume. 

Volume of sphere = Volume of cylinder

Hence, the height of the cylinder so formed will be 2.74 cm.

19. Metallic spheres of radii 6 cm, 8 cm, and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.

Answer:

Radius (r₁) of 1^st sphere = 6 cm 

Radius (r₂) of 2^nd sphere = 8 cm 

Radius (r₃) of 3^rd sphere = 10 cm 

Let the radius of the resulting sphere be r. 

The object formed by recasting these spheres will be same in volume as the sum of the volumes of these spheres. 

Volume of 3 spheres = Volume of resulting sphere

Therefore, the radius of the sphere so formed will be 12 cm.

20. A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.  [Use \(\pi\) = 22/7]

Answer:

The shape of the well will be cylindrical. 

Depth (h) of well = 20 m 

Radius (r) of circular end of well = 7/2 cm 

Area of platform = Length × Breadth = 22 × 14 m² 

Let height of the platform = H 

Volume of soil dug from the well will be equal to the volume of soil scattered on the platform.

Volume of soil from well = Volume of soil used to make such platform

\(\pi \) x r² x h = Area of platform x Height of platform

Therefore, the height of such platform will be 2.5 m.

21. A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.

Answer:

The shape of the well will be cylindrical. 

Depth (h₁) of well = 14 m 

Radius (r₁) of the circular end of well = 3/2 m 

Width of embankment = 4 m 

From the figure, it can be observed that our embankment will be in a cylindrical shape having outer radius (r₂) as 4+ (3/2) = 11/2 m and inner radius (r₁) as 3/2 m. 

Let the height of embankment be h₂.

Volume of soil dug from well = Volume of earth used to form embankment

Therefore, the height of the embankment will be 1.125 m.

22. A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.

Answer:

Height (h₁) of cylindrical container = 15 cm 

Radius (r₁) of circular end of container = 6 cm 

Radius (r₂) of circular end of ice-cream cone = 3 cm 

Height (h₂) of conical part of ice-cream cone = 12 cm 

Let n ice-cream cones be filled with ice-cream of the container. 

Volume of ice-cream in cylinder = n × (Volume of 1 ice-cream cone + Volume of hemispherical shape on the top)

Therefore, 10 ice-cream cones can be filled with the ice-cream in the container.

23. How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm ×10 cm × 3.5 cm? [Use \(\pi\) = 22/7]

Answer:

Coins are cylindrical in shape. 

Height (h₁) of cylindrical coins = 2 mm = 0.2 cm

Radius (r) of circular end of coins = 1.75/2 = 0.875 cm 

Let n coins be melted to form the required cuboids. 

Volume of n coins = Volume of cuboids

Therefore, the number of coins melted to form such a cuboid is 400.

Answer 4

24. A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm. Find the radius and slant height of the heap.

Answer:

Height (h₁) of cylindrical bucket = 32 cm 

Radius (r₁) of circular end of bucket = 18 cm 

Height (h₂) of conical heap = 24 cm 

Let the radius of the circular end of conical heap be r₂. 

The volume of sand in the cylindrical bucket will be equal to the volume of sand in the conical heap. 

Volume of sand in the cylindrical bucket = Volume of sand in conical heap

Therefore, the radius and slant height of the conical heap are 36 cm and 12\(\sqrt{13}\) cm respectively.

25. Water in canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. how much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?

Answer:

Consider an area of cross-section of canal as ABCD. 

Area of cross-section = 6 × 1.5 = 9 m² 

Speed of water = 10 km/h = \(\frac{1000}{60}\) m/min 

Volume of water that flows in 1 minute from canal = 9 × \(\frac{1000}{60}\) =1500 m³ 

Volume of water that flows in 30 minutes from canal = 30 × 1500 = 45000 m³

Let the irrigated area be A. Volume of water irrigating the required area will be equal to the volume of water that flowed in 30 minutes from the canal. 

Volume of water flowing in 30 minutes from canal = Vol. of water irrigating the reqd. area

\(45000=\frac{A\times8}{100}\)

A = 562500 m² 

Therefore, area irrigated in 30 minutes is 562500 m².

26. A farmer connects a pipe of internal diameter 20 cm form a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?

Answer:

Consider an area of cross-section of pipe as shown in the figure. 

Radius (r₁) of circular end of pipe = 20/200 = 0.1 m 

Area of cross-section = \(\pi {r_1}^2\) = (0.1)² = 0.01π m³ 

Speed of water = 3 km/h = 3000/60 = 50 m/min 

Volume of water that flows in 1 minute from pipe = 50 × 0.01π = 0.5π m³

Volume of water that flows in t minutes from pipe = t × 0.5π m³

Radius (r₂) of circular end of cylindrical tank = 5m

Depth (h₂) of cylindrical tank = 2 m 

Let the tank be filled completely in t minutes. 

Volume of water filled in tank in t minutes is equal to the volume of water flowed in t minutes from the pipe. 

Volume of water that flows in t minutes from pipe = Volume of water in tank

Therefore, the cylindrical tank will be filled in 100 minutes.

27. A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [Use π = 22/7]

Answer:

Radius (r₁) of upper base of glass = 4/2 = 2 cm 

Radius (r₂) of lower base of glass = 2/2 = 1 cm 

Capacity of glass = Volume of frustum of cone

Therefore, the capacity of the glass is \(102\frac{2}3{}\) cm³.

28. The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. find the surface area of the frustum.

Answer:

Perimeter of upper circular end of frustum = 18 

2πr₁ =18

\(r_1=\frac{9}{\pi}\)

Perimeter of lower end of frustum = 6 cm 

2πr₂ = 6

\(r_2=\frac{3}{\pi}\)

Slant height (l) of frustum = 4 

CSA of frustum = π (r₁ + r₂) l

= \(\pi (\frac{9}{\pi}+\frac{3}{\pi})4\)

= 12 x 4

= 48 cm²

Therefore, the curved surface area of the frustum is 48 cm².

29. A fez, the cap used by the Turks, is shaped like the frustum of a cone (see the figure given below). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material use for making it. [Use π = 22/7]

Answer:

Radius (r₂) at upper circular end = 4 cm 

Radius (r₁) at lower circular end = 10 cm 

Slant height (l) of frustum = 15 cm 

Area of material used for making the fez = CSA of frustum + Area of upper circular end

= \(\pi (r_1 + r_2)l + \pi {r_2}^2\)

= π (10 + 4) 15 + π (4)²

= π (14) 15 + 16 π

= 210π + 16π

= \(\frac{226\times22}{7}\)

= \(710\frac{2}{7}\) cm²

Therefore, the area of material used for making it is \(710\frac{2}{7}\) cm².

Answer 5

30. A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs.20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs.8 per 100 cm² . [Take π = 3.14]

Answer:

Radius (r₁) of upper end of container = 20 cm 

Radius (r₂) of lower end of container = 8 cm 

Height (h) of container = 16 cm 

Slant height of the frustum 

Capacity of container = Volume of frustum

Cost of 1 litre milk = Rs 20 

Cost of 10.45 litre milk = 10.45 × 20 = Rs 209 

Area of metal sheet used to make the container

= \(\pi (r_1 + r_2)l + \pi {r_2}^2\)

= π (20 + 8) 20 + π (8)² 

= 560 π + 64 π = 624 π cm² 

Cost of 100 cm² metal sheet = Rs 8

Cost of 624 π cm² metal sheet = \(\frac{624\times3.14\times8}{100}\)

= 156.75

Therefore, the cost of the milk which can completely fill the container is Rs 209 and the cost of metal sheet used to make the container is Rs 156.75.

31. A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire. [Use π = 22/7]

Answer:

In ∆AEG,

In ∆ABD,

Radius (r₁) of upper end of frustum = \(\frac{10\sqrt{3}}{3}\) cm

Radius (r₂) of lower end of container = \(\frac{20\sqrt{3}}{3}\) cm

Height (h) of container = 10 cm

Volume of frustum

Radius (r) of wire = \(\frac{1}{16}\times\frac{1}{2}=\frac{1}{32}\) cm

Let the length of wire be l. 

Volume of wire = Area of cross-section × Length 

= (πr²) (l)

= \(\pi (\frac{1}{32})^2 \times l\)

Volume of frustum = Volume of wire

32. A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm³.

Answer:

It can be observed that 1 round of wire will cover 3 mm height of cylinder.

\(Numbers \, of\, rounds=\frac{Height\, of \,cylinder}{Diameter \, of \,wire}\)

= \(\frac{12}{0.3}\)

= 40 rounds

Length of wire required in 1 round = Circumference of base of cylinder 

= 2πr = 2π × 5 = 10π 

Length of wire in 40 rounds = 40 × 10π

= \(\frac{400\times22}{7}\)

= \(\frac{8800}{7}\)

= 1257.14 cm = 12.57 m 

Radius of wire = 0.15 cm 

Volume of wire = Area of cross-section of wire × Length of wire 

= π(0.15)² × 1257.14 

= 88.898 cm³ 

Mass = Volume × Density 

= 88.898 × 8.88 

= 789.41 gm

33. A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)

Answer:

The double cone so formed by revolving this right-angled triangle ABC about its hypotenuse is shown in the figure.

Hypotenuse AC = \(\sqrt{3^2+4^2} \)

= \(\sqrt{25} \)

= 5 cm

Area of ∆ABC

Volume of double cone = Volume of cone 1 + Volume of cone 2

= 30.14 cm³ 

Surface area of double cone = Surface area of cone 1 + Surface area of cone 2 

= πrl₁ + πrl₂

= πr [4 + 3] = 3.14 x 2.4 x 7

= 52.75 cm²

34. A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm³ of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?

Answer:

Volume of cistern = 150 × 120 × 110 = 1980000 cm³

Volume to be filled in cistern = 1980000 − 129600 = 1850400 cm³ 

Let n numbers of porous bricks were placed in the cistern. 

Volume of n bricks = n × 22.5 × 7.5 × 6.5 = 1096.875n 

As each brick absorbs one-seventeenth of its volume, therefore, volume absorbed by these bricks

n = 1792.41

Therefore, 1792 bricks were placed in the cistern.

35. In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 97280 km² , show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.

Answer:

Rainfall in the river valley = 10 cm = 0.1 m 

Area of the river valley = 97280 km² = 97280000000 m² 

Volume of the water = 97280000000 × 0.1 = 9728000000 m³ 

Now volume of one river water = 1072000 × 75×3 = 241200000 m³ 

Now volume of 3 rivers water = 3 × 241200000 = 843600000 m³ 

So,

 9728000000 m³ ≈ 843600000 m³

Answer 6

36. An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).

Answer:

Radius (r₁) of upper circular end of frustum part 9 cm.

Radius (r₂) of lower circular end of frustum part = Radius of circular end of cylindrical part = 4 cm 

Height (h₁) of frustum part = 22 − 10 = 12 cm 

Height (h₂) of cylindrical part = 10 cm 

Slant height (l) of frustum part

Area of tin sheet required = CSA of frustum part + CSA of cylindrical part

37. Derive the formula for the curved surface area and total surface area of the frustum of cone.

Answer:

Let ABC be a cone. A frustum DECB is cut by a plane parallel to its base. 

Let r₁ and r₂ be the radii of the ends of the frustum of the cone and h be the height of the frustum of the cone. 

In ∆ABG and ∆ADF, 

DF||BG 

∴ ∆ABG ∼ ∆ADF

CSA of frustum DECB = CSA of cone ABC − CSA cone ADE

CSA of frustum = \(\pi (r_1+r_2)l\)

Total surface area of frustum = CSA of frustum + Area of upper circular end + Area of lower circular end

38. Derive the formula for the volume of the frustum of a cone.

Answer:

Let ABC be a cone. A frustum DECB is cut by a plane parallel to its base. Let r₁ and r₂ be the radii of the ends of the frustum of the cone and h be the height of the frustum of the cone. 

In ∆ABG and ∆ADF, 

DF||BG 

∴ ∆ABG ∼ ∆ADF

Volume of frustum of cone = Volume of cone ABC − Volume of cone ADE