16. How much should the pressure on a litre of water be changed to compress it by 0.10%?
Solution:
Volume of water, V = 1 L
It is given that water is to be compressed by 0.10%.
∴ Fractional change, \(\frac {△V}{V}\) = \(\frac {0.1}{100\times1}= 10^{-3}\)
Bulk modulus, B = \(\frac {\frac P{△V}}{V}\)
p = B x \(\frac {△V}{V}\)
Bulk modulus of water, B = 2.2 x 109 Nm-2
p = 2.2 x 109 x 10-3
= 2.2 x 106 Nm-2
Therefore, the pressure on water should be 2.2 ×106 Nm–2.
17. Anvils made of single crystals of diamond, with the shape as shown in Figure, are used to investigate behaviour of materials under very high pressures. Flat faces at the narrow end of the anvil have a diameter of 0.50 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil?

Solution:
Diameter of the cones at the narrow ends, d = 0.50 mm = 0.5 × 10–3 m
Radius, r = \(\frac d2\) = 0.25 x 10-3m
Compressional force, F = 50000 N
Pressure at the tip of the anvil:
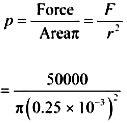
= 2.55 x 1011 Pa
Therefore, the pressure at the tip of the anvil is 2.55 × 1011 Pa.
18. A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Figure. The cross sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2 , respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
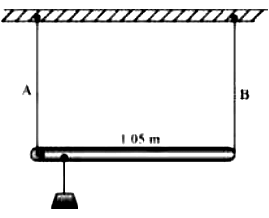
Solution:
(a) 0.7 m from the steel-wire end 0.432 m from the steel-wire end
Cross-sectional area of wire A, a1 = 1.0 mm2 = 1.0 × 10–6 m2
Cross-sectional area of wire B, a2 = 2.0 mm2 = 2.0 × 10–6 m2
Young’s modulus for steel, Y1 = 2 × 1011 Nm–2
Young’s modulus for aluminium, Y2 = 7.0 ×1010 Nm–2
Let a small mass m be suspended to the rod at a distance y from the end where wire A is attached.
Stress in the wire = \(\frac {Force}{Area} = \frac Fa\)
If the two wires have equal stresses, then:
\(\frac {F_1}{a_1} = \frac {F_2}{a_2} \)
Where,
F1 = Force exerted on the steel wire
F2 = Force exerted on the aluminum wire

The situation is shown in the following figure.
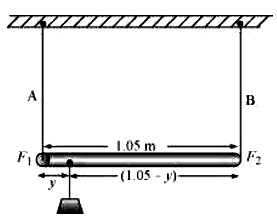
Taking torque about the point of suspension, we have:

Using equations (i) and (ii), we can write:
\(\frac {(1.05-y)}{y} = \frac 12\)
2(1.05-y) = y
2.1 - 2y = y
3y = 2.1
∴ y = 0.7m
In order to produce an equal stress in the two wires, the mass should be suspended at a distance of 0.7 m from the end where wire A is attached.
Young's modulus = \(\frac {Stress}{Strain}\)
Strain = \(\frac {Stress}{Young's\, modulus} = \frac {\frac Fa}{Y}\)
If the strain in the two wires is equal, then:
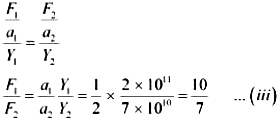
Taking torque about the point where mass m, is suspended at a distance y1 from the side where wire A attached, we get:
F1y1 = F2 (1.05 – y1)
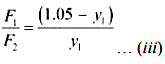
Using equations (iii) and (iv), we get:
\(\frac {(1.05-y_1)}{y_1} = \frac {10}7\)
7(1.05-y1) = 10y1
17 y1 = 7.35
∴ y1 = 0.432 m
In order to produce an equal strain in the two wires, the mass should be suspended at a distance of 0.432 m from the end where wire A is attached.
19. A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10–2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
Solution:

Length of the steel wire = 1.0 m
Area of cross-section, A = 0.50 x 10-2 cm2 = 0.50 x 10-6 m2
A mass 100g is suspended from its midpoint
m = 100g = 0.1 kg
Hence, the wire dips, as shown in the given figure.
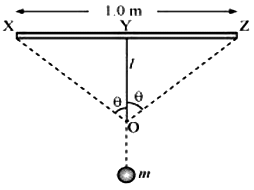
Original length = XZ
Depression = l
The length after mass m, is attached to the wire = XO + OZ
Increase in the length of the wire:
Δl = (XO + OZ) – XZ
Where,

Expanding and neglecting higher terms, we get:
Δl = \(\frac {l^2}{0.5}\)
Strain = \(\frac {Increase \, in\, length}{Original\, length}\)
Let T be the tension in the wire.
∴ mg = 2T cosθ
Using the figure, it can be written as:

Expanding the expression and eliminating the higher terms:

Young's modulus = \(\frac {Stress}{Strain}\)

Young’s modulus of steel, Y = 2 x 1011 Pa

= 0.0106 m
Hence, the depression at the midpoint is 0.0106 m.