Question

NCERT Solutions Class 11 Maths Chapter 13 Limits and Derivatives have one-step solutions to all the question-answers related to Limits and Derivatives. Our NCERT Solutions have discussed all the concepts thoroughly.

Our NCERT Solutions Class 11 provides a holistic approach to learning new concepts. Important concepts discussed in the chapter are:

• Limits – limit is the value that a sequence or a function tends to approach when the input approaches some value. Limits are one of the most important parts of modern mathematics it helps in performing important calculations in calculus, mathematical analysis, continuity, derivative, and integrals. If f(y) is a given function, then the limit of the function can be represented as lim_y→c.
• Derivatives – a derivative is the rate of change of one function or quantity concerning other independent variables. Derivatives are mainly used when there is any variable quantity, and the rate of change of the derivative is not constant. Derivatives also help us measure the sensitivity of a dependent variable concerning another independent variable.
• Limits of the trigonometric functions – there are six trigonometric functions. The limit of each function tending to a point can be calculated with the help of the function’s continuity by its domain and range.
  • Sine function - The function f(x) = sin(x) is a continuous function over its complete domain, with its domain having all the real numbers. The range of the sine function is [-1,1].
  • Cosine function - The function f(x) = cos(x) is a continuous function over its complete domain, with its domain having all the real numbers. The range of the Cosine function is [-1,1].
  • Tangent function - The function f(x) = tan(x) is defined for all real numbers except the values where cos(x) is equal to 0, that is, the values\({\pi \over 2} + \pi n\) for all integers n. Hence, its domain is all real numbers except \({\pi \over 2} + \pi n\), \(n\in Z\). The range of this function lies in (-\(\infty \), +c).

Our NCERT Solutions Class 11 Maths discusses important topics such as limits and derivatives. Our subject matter suggests students learn all concepts thoroughly.

Answer 1

NCERT Solutions Class 11 Maths Chapter 13 Limits and Derivatives

1. Evaluate the Given limit: 

 \(\lim\limits_{x\to3}x+3\)

Answer:

\(\lim\limits_{x\to3}x+3= 3 + 3=6\)

2. Evaluate the Given limit:

\(\lim\limits_{x\to\pi}\left(x-\frac{22}{7}\right)\)

Answer:

\(\lim\limits_{x\to\pi}\left(x-\frac{22}{7}\right)= \left(\pi-\frac{22}{7}\right)\)

3. Evaluate the Given limit:

\(\lim\limits_{r\to1}\pi r^2\)

Answer:

\(\lim\limits_{r\to1}\pi r^2=\pi(1)^2=\pi\) 

4. Evaluate the Given limit:

\(\lim\limits_{x\to4}\frac{4x+3}{x-2}\)

Answer:

5. Evaluate the Given limit:

\(\lim\limits_{x\to-1}\frac{x^{10}+ x^5+1}{x-1}\)

Answer:

6. Evaluate the Given limit:

\(\lim\limits_{x\to0}\frac{(x+1)^5-1}{x}\)

Answer:

\(\lim\limits_{x\to0}\frac{(x+1)^5-1}{x}\)

Put x + 1 = y so that y → 1 as x → 0.

Accordingly,

∴ \(\lim\limits_{x\to0}\frac{(x+1)^5-1}{x}=5\) 

7. Evaluate the Given limit:

\(\lim\limits_{x\to2}\frac{3x^2-x-10}{x^2-4}\)

Answer:

At x = 2, the value of the given rational function takes the form. \(\frac00\)

8. Evaluate the Given limit:

\(\lim\limits_{x\to3}\frac{x^4-81}{2x^2-5x-3}\)

Answer:

At x = 2, the value of the given rational function takes the form. \(\frac00\)

9 Evaluate the Given limit:

\(\lim\limits_{x\to0}\frac{ax+b}{cx+1}\)

Answer:

\(\lim\limits_{x\to0}\frac{ax+b}{cx+1}=\frac{a(0)+b}{c(0)+1}=b\)

10. Evaluate the Given limit: 

\(\lim\limits_{x\to1}\cfrac{z^{\frac13}-1}{z^{\frac16}-1}\)

Answer:

\(\lim\limits_{x\to1}\cfrac{z^{\frac13}-1}{z^{\frac16}-1}\) 

At z = 1, the value of the given function takes the form. \(\frac00\)

Put \(z^{\frac16}=x\) so that z →1 as x → 1.

Accordingly,

\(\lim\limits_{x\to1}\cfrac{z^{\frac13}-1}{z^{\frac16}-1}= 2\)

11. Evaluate the Given limit: 

\(\lim\limits_{x\to1}\frac{ax^2+bx+c}{cx^2+bx+a},a+b+bc\ne0\)

Answer:

12. Evaluate the Given limit:

\(\lim\limits_{x\to2}\cfrac{\frac1x+\frac12}{x+2}\)

Answer:

\(\lim\limits_{x\to2}\cfrac{\frac1x+\frac12}{x+2}\)

At x = –2, the value of the given function takes the form. \(\frac00\)

Now,

13. Evaluate the Given limit:

\(\lim\limits_{x\to0}\frac{sin\, ax}{bx}\)

Answer:

\(\lim\limits_{x\to0}\frac{sin\, ax}{bx}\)

At x = 0, the value of the given function takes the form. \(\frac00\)

Now,

14. Evaluate the Given limit: 

\(\lim\limits_{x\to0}\frac{sin\, ax}{sin\,bx},a,b\ne0\)

Answer:

\(\lim\limits_{x\to0}\frac{sin\, ax}{sin\,bx},a,b\ne0\)

At x = 0, the value of the given function takes the form. \(\frac00\)

Now,

15. Evaluate the Given limit: 

\(\lim\limits_{x\to\pi}\left(\frac{sin(\pi-x)}{\pi(\pi-x)}\right)\)

Answer:

\(\lim\limits_{x\to\pi}\left(\frac{sin(\pi-x)}{\pi(\pi-x)}\right)\)

It is seen that x → π ⇒ (π – x) → 0

16. Evaluate the given limit: 

\(\lim\limits_{x\to0}\frac{cos\, ax}{\pi-x}\)

Answer:

\(\lim\limits_{x\to0}\frac{cos\, ax}{\pi-x}=\frac{cos\,0}{\pi-0}=\frac1{\pi}\) 

17. Evaluate the Given limit: 

\(\lim\limits_{x\to0}\frac{cos\, 2x-1}{cos\, x -1}\) 

Answer:

\(\lim\limits_{x\to0}\frac{cos\, 2x-1}{cos\, x -1}\) 

At x = 0, the value of the given function takes the form. \(\frac00\)

Now,

18. Evaluate the Given limit:

\(\lim\limits_{x\to0}\frac{ax + x\,cos\,x}{b\,sin\,x}\) 

Answer:

\(\lim\limits_{x\to0}\frac{ax + x\,cos\,x}{b\,sin\,x}\)

At x = 0, the value of the given function takes the form. \(\frac00\)

Now,

19. Evaluate the Given limit:

\(\lim\limits_{x\to0}x\,sec\,x\) 

Answer:

\(\lim\limits_{x\to0}x\,sec\,x= \lim_\limits{x\to0}\frac x{cos\,x}=\frac0{cos\,0}=\frac01=0\) 

Answer 2

20. Evaluate the Given limit:

\(\lim\limits_{x\to0}\frac{sin\, ax+bx}{ax+sin\,bx},a,b,a+b\ne0\)

Answer:

At x = 0, the value of the given function takes the form. \(\frac00\)

Now,

21. Evaluate the Given limit:

\(\lim\limits_{x\to0}(cosec \,x -cot\,x)\)

Answer:

At x = 0, the value of the given function takes the form. \(\infty-\infty\)

Now,

22. Evaluate the Given limit:

Answer:

At \(x=\frac{\pi}2\), the value of the given function takes the form \(\frac00\).

Now \(x-\frac{\pi}2=y\), put so that \(x\to\frac{\pi}2,y\to0\)

23. Find:

Answer:

The given function is f(x) = 

24. Find: \(\lim_\limits{x\to1}\) f(x), where f(x) =

Answer:

The given function is

It is observed that \(\lim_\limits{x\to1}\) f(x).

Hence, \(\lim_\limits{x\to1}\) f(x) does not exist.

25. Evaluate \(\lim_\limits{x\to0}\) f(x), where f(x) =

Answer:

The given function is f(x) = 

It is observed that \(\lim_\limits{x\to0^-}f(x)\ne\) \(\lim_\limits{x\to0^+}f(x)\) 

Hence, \(\lim_\limits{x\to0}f(x)\) does not exist.

26. Find   \(\lim_\limits{x\to0}\) f(x), where f(x) =

Answer:

The given function is

It is observed that  \(\lim_\limits{x\to0^-}f(x)\ne\) \(\lim_\limits{x\to0^+}f(x)\) 

Hence, \(\lim_\limits{x\to0}f(x)\) does not exist.

27. Find \(\lim_\limits{x\to5}\) f(x), where f(x) = |x| - 5

Answer:

The given function is f(x) = |x| - 5

28. Suppose f(x) = 

and \(\lim_\limits{x\to1}\) f(x) = f(1) what are possible values of a and b?

Answer:

The given function is

On solving these two equations, we obtain a = 0 and b = 4.

Thus, the respective possible values of a and b are 0 and 4.

29. Let a₁, a₂, . . ., a_n be fixed real numbers and define a function 

f(x) = (x − a₁) (x − a₂)...(x − a_n) .

What is \(\lim_\limits{x\to a_1}\) f(x) ? For some a ≠ a₁, a₂... a_n, compute \(\lim_\limits{x\to a}\) f(x).

Answer:

The given function is f(x) = (x − a₁) (x − a₂)...(x − a_n)

30. If f(x) = 

For what value(s) of a does \(\lim_\limits{x\to a}\) f(x) exists?

Answer:

The given function is

When a = 0,

Here, it is observed that  \(\lim_\limits{x\to0^-}f(x)\ne\) \(\lim_\limits{x\to0^+}f(x)\) 

∴ \(\lim_\limits{x\to0}f(x)\) does not exist.

When a < 0,

Thus, limit of f(x) exists at x = a, where a < 0.

When a > 0,

Thus, \(\lim_\limits{x\to0}f(x)\) exists for all a ≠ 0.

31. If the function f(x) satisfies, \(\lim_\limits{x\to1}\frac{f(x)-2}{x^2-1}=\pi\) evaluate \(\lim_\limits{x\to1}f(x)\) 

Answer:

\(\lim_\limits{x\to1}\frac{f(x)-2}{x^2-1}=\pi\) 

Answer 3

32. If.

For what integers m and n does \(\lim_\limits{x\to0}f(x)\) and \(\lim_\limits{x\to1}f(x)\) exist?

Answer:

The given function is

Thus \(\lim_\limits{x\to1}f(x)\) exist for any integral value of m and n.

33. Find the derivative of x² – 2 at x = 10.

Answer:

Let f(x) = x² – 2. 

Accordingly,

Thus, the derivative of x² – 2 at x = 10 is 20.

34. Find the derivative of 99x at x = 100.

Answer:

Let f(x) = 99x. 

Accordingly,

Thus, the derivative of 99x at x = 100 is 99.

35. Find the derivative of x at x = 1.

Answer:

Let f(x) = x. 

Accordingly,

Thus, the derivative of x at x = 1 is 1.

36. Find the derivative of the following functions from first principle. 

(i) x³ – 27 

(ii) (x – 1) (x – 2)

(iii) \(\frac1{x^2}\)

(iv) \(\frac{x+1}{x-1}\)

Answer:

(i) Let f(x) = x³ – 27. 

Accordingly, from the first principle,

(ii) Let f(x) = (x – 1) (x – 2). 

Accordingly, from the first principle,

(iii) Let \(\frac1{x^2}\) 

Accordingly, from the first principle,

(iv) Let \(\frac{x+1}{x-1}\). 

Accordingly, from the first principle,

37. For the function 

\(f(x)=\frac{x^{100}}{100}+\frac{x^{99}}{99}+...+\frac{x^2}{2}+x+1\)

Prove that f'(1) = 100 f'(0)

Answer:

The given function is

\(f(x)=\frac{x^{100}}{100}+\frac{x^{99}}{99}+...+\frac{x^2}{2}+x+1\) 

On using theorem \(\frac d{dx}(x^n)=nx^{-1},\) we obtain

Thus, f'(1) = 100 f'(0)

38. Find the derivative of xⁿ + ax^n-1 + a²x^n-2 + ... + a^n-1x + aⁿ for some fixed real number a.

Answer:

Let f(x) = xⁿ + ax^n-1 + a²x^n-2 + ... + a^n-1x + aⁿ

On using theorem \(\frac d{dx}(x^n)=nx^{-1},\) we obtain

39. For some constants a and b, find the derivative of 

(i) (x – a) (x – b) 

(ii) (ax² + b)² 

(iii) \(\frac{x-a}{x-b}\) 

Answer:

(i) Let f(x) = (x – a) (x – b)

On using theorem \(\frac d{dx}(x^n)=nx^{-1},\) we obtain

f'(x) = 2x - (a + b) + 0 = 2x - a - b

(ii) Let f(x) = (ax² + b)² 

On using theorem \(\frac d{dx}(x^n)=nx^{-1},\) we obtain

(iii) Let f(x) = \(\frac{x-a}{x-b}\) 

By quotient rule,

40. Find the derivative of \(\frac{x^n-a^n}{x-a}\) for some constant a.

Answer:

Let f(x) = \(\frac{x^n-a^n}{x-a}\)

By quotient rule,

Answer 4

41. Find the derivative of

(i) \(2x - \frac34\)

(ii) (5x³ + 3x – 1) (x – 1) 

(iii) x^–3 (5 + 3x) 

(iv) x⁵ (3 – 6x^–9) 

(v) x^–4 (3 – 4x^–5)

(vi) \(\frac{2}{x+1}-\frac{x^2}{3x-1}\) 

Answer:

(i) Let f(x) = \(2x - \frac34\) 

(ii) Let f (x) = (5x³ + 3x – 1) (x – 1)

By Leibnitz product rule,

(iii) Let f (x) = x^–3 (5 + 3x)

By Leibnitz product rule,

(iv) Let f (x) = x⁵ (3 – 6x^–9)

By Leibnitz product rule,

(v) Let f (x) = x^–4 (3 – 4x^–5)

 By Leibnitz product rule,

(vi) Let f (x) = \(\frac{2}{x+1}-\frac{x^2}{3x-1}\) 

By quotient rule,

42. Find the derivative of cos x from first principle.

Answer:

Let f (x) = cos x.

 Accordingly, from the first principle,

∴ f'(x) = - sin x

43. Find the derivative of the following functions: 

(i) sin x cos x 

(ii) sec x 

(iii) 5 sec x + 4 cos x 

(iv) cosec x 

(v) 3cot x + 5cosec x 

(vi) 5sin x – 6cos x + 7 

(vii) 2tan x – 7sec x

Answer:

(i) Let f (x) = sin x cos x.

Accordingly, from the first principle,

(ii) Let f (x) = sec x. 

Accordingly, from the first principle,

(iii) Let f (x) = 5 sec x + 4 cos x. 

Accordingly, from the first principle,

(iv) Let f (x) = cosec x. 

Accordingly, from the first principle,

 

(v) Let f (x) = 3cot x + 5cosec x. 

Accordingly, from the first principle,

From (1), (2), and (3), we obtain

f'(x) = -3cosc²x - 5cosec x cot x

(vi) Let f (x) = 5sin x – 6cos x + 7. 

Accordingly, from the first principle,

(vii) Let f (x) = 2 tan x – 7 sec x. 

Accordingly, from the first principle,

44. Find the derivative of the following functions from first principle: 

(i) –x 

(ii) (–x)–1 

(iii) sin (x + 1)

(iv) \(cos(x-\frac{\pi}8)\) 

Answer:

(i) Let f(x) = –x.

Accordingly, f(x + h) = - (x + h)

By first principle,

(ii) Let f(x) = (-x)^-1 = \(\frac{1}{-x}=\frac{-1}x\). 

Accordingly,

(iii) Let f(x) = sin (x + 1). 

Accordingly, f(x + h) = sin (x + h + 1)

By first principle,

(iv) Let f(x) = \(cos(x-\frac{\pi}8)\). 

Accordingly, f(x + h) = \(cos(x+h-\frac{\pi}{8})\)

By first principle,

45. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x + a)

Answer:

Let f(x) = x + a. 

Accordingly, f(x + h) = x + h + a

By first principle,

46. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \((px+q)(\frac rx+s)\) 

Answer:

Let f(x) = \((px+q)(\frac rx+s)\) 

47. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers)

Answer:

Let f(x) = (ax + b) (cx + d)²

By product rule,

48. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{ax+b}{cx+d}\)

Answer:

Let f(x) = \(\frac{ax+b}{cx+d}\) 

Answer 5

49. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): 

\(\cfrac{1+\frac1x}{1-\frac1x}\)

Answer:

By quotient rule,

50. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac1{ax^2+bx+c}\) 

Answer:

Let f(x) = \(\frac{1}{ax^2+bx+c}\) 

By quotient rule,

51. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{ax+b}{px^2+qx+r}\)

Answer:

Let f(x) = \(\frac{ax+b}{px^2+qx+r}\) 

By quotient rule,

52. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{px^2+qx+r}{ax+b}\)

Answer:

Let f(x) = \(\frac{px^2+qx+r}{ax+b}\) 

By quotient rule,

53. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac a{x^4}-\frac b{x^2}+cos \,x\)

Answer:

Let f(x) = \(\frac a{x^4}-\frac b{x^2}+cos \,x\) 

54. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): 4√x - 2

Answer:

Let (x) = 4√x - 2

 

55. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax + b)ⁿ

Answer:

Let f(x) = (ax + b)ⁿ .

Accordingly,

f(x + h) = {a(x + h) + b}ⁿ = (ax + ah + b)ⁿ 

By first principle,

56. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax + b)ⁿ (cx + d)^m

Answer:

Let f(x) = (ax + b)ⁿ (cx + d)^m

Therefore, from (1), (2), and (3), we obtain

57. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): sin (x + a)

Answer:

Let f(x) = sin (x + a), therefore f(x + h) = sin (x + h + a)

By first principle,

58. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): cosec x cot x

Answer:

Let f(x) = cosec x cot x

By product rule,

By first principle,

Now, let f₂(x) = cosec x. 

Accordingly, f₂(x + h) = cosec(x + h)

By first principle,

From (1), (2), and (3), we obtain

59. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{cos\, x}{1 + sin \, x}\) 

Answer:

Let f(x) = \(\frac{cos\, x}{1 + sin \, x}\) 

By quotient rule,

60. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{sin\, x+cos\, x}{sin\,x-cos\,x}\) 

Answer:

Let f(x) = \(\frac{sin\, x+cos\, x}{sin\,x-cos\,x}\) 

61. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{sec\,x-1}{sec\,x+1}\)

Answer:

Let f(x) = \(\frac{sec\,x-1}{sec\,x+1}\) 

By quotient rule,

Answer 6

62. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): sinⁿ x

Answer:

Let y = sinⁿ x. 

Accordingly, for n = 1, y = sin x.

For n = 2, y = sin² x.

For n = 3, y = sin³ x.

We assert that

Let our assertion be true for n = k.

i.e.,

Consider

Thus, our assertion is true for n = k + 1. 

Hence, by mathematical induction,

63. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{a + b\,sin\,x}{c+d\,cos\,x}\) 

Answer:

Let f(x) = \(\frac{a + b\,sin\,x}{c+d\,cos\,x}\) 

By quotient rule,

64. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{sin(x+a)}{cos\,x}\)

Answer:

Let f(x) = \(\frac{sin(x+a)}{cos\,x}\) 

By quotient rule,

Let g(x) = sin(x + a), Accordingly, g(x + h) = sin (x + h + a)

By first principle,

From (i) and (ii), we obtain

65. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): x⁴ (5 sin x – 3 cos x)

Answer:

Let f(x) = x⁴ (5 sin x – 3 cos x)

By product rule,

66. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x² + 1) cos x

Answer:

Let f(x) = (x² + 1) cos x

By product rule,

67. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (ax² + sin x) (p + q cos x)

Answer:

Let f(x) = (ax² + sin x) (p + q cos x)

By product rule,

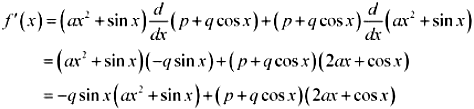
68. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x + cos x) (x - tan x)

Answer:

Let f(x) =(x + cos x) (x - tan x)

By product rule,

Let g(x) = tan x. Accordingly, g(x +h) = tan(x + h)

By first principle,

Therefore, from (i) and (ii), we obtain

69. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{4x+5\,sin\,x}{3x+7\,cos\,x}\)

Answer:

Let f(x) = \(\frac{4x+5\,sin\,x}{3x+7\,cos\,x}\) 

By quotient rule,

70. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{x^2\,cos(\frac{\pi}4)}{sin \,x}\)

Answer:

Let f(x) = \(\frac{x^2\,cos(\frac{\pi}4)}{sin \,x}\) 

By quotient rule,

71. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac{x}{1+tan\, x}\)

Answer:

Let f(x) = \(\frac{x}{1+tan\, x}\) 

Let g(x) = 1 + tan x.

Accordingly, g(x + h) = 1 + tan (x + h).

By first principle,

From (i) and (ii), we obtain

72. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): (x + sec x) (x – tan x)

Answer:

Let f(x) = (x + sec x) (x – tan x)

By product rule,

Let f₁(x) = tan x, f₂(x) = sec x

Accordingly, f₁(x + h) = tan(x + h) and f₂(x + h) = sec(x + h)

From (i), (ii), and (iii), we obtain

f'(x) = (x + sec x) (1 - sec²x) + (x - tan x) (1 + sec x tan x)

Answer 7

73. Find the derivative of the following functions (it is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants and m and n are integers): \(\frac x{sin^n\,x}\)

Answer:

Let f(x) = \(\frac x{sin^n\,x}\)

By quotient rule,

It can be easily shown that \(\frac{d}{dx}sin^n \, x=n\,sin^{n-1}\,x\,cos\,x\)

Therefore,

74. Evaluate the limits, if exist.

\(\lim_\limits{x\to0}\frac{e^{4x}-1}{x}\)

Answer:

\(\lim_\limits{x\to0}\frac{e^{4x}-1}{x}\)

75. Evaluate the limits, if exist.

\(\lim_\limits{x\to0}\frac{e^{2+x}-e^2}{x}\)

Answer:

\(\lim_\limits{x\to0}\frac{e^{2+x}-e^2}{x}\)

76. Evaluate the limits, if exist.

\(\lim_\limits{x\to5}\frac{e^{x}-e^5}{x-5}\)

Answer:

\(\lim_\limits{x\to5}\frac{e^{x}-e^5}{x-5}\)

Put x = 5 + h, then as x → 5 ⇒ h → 0.

Therefore,

77. Evaluate the limits, if exist.

\(\lim_\limits{x\to0}\frac{e^{sin\,x}-1}{x}\)

Answer:

\(\lim_\limits{x\to0}\frac{e^{sin\,x}-1}{x}\)

78. Evaluate the limits, if exist.

\(\lim_\limits{x\to3}\frac{e^{x}-e^3}{x-3}\)

Answer:

\(\lim_\limits{x\to3}\frac{e^{x}-e^3}{x-3}\)

Put x = 3 + h, then as x → 3 ⇒ h → 0.

Therefore,

79. Evaluate the limits, if exist.

\(\lim_\limits{x\to0}\frac{x(e^x-1)}{1-cos\,x}\)

Answer:

\(\lim_\limits{x\to0}\frac{x(e^x-1)}{1-cos\,x}\)

80. Evaluate the limits, if exist.

\(\lim_\limits{x\to0}\frac{log_e(1+2x)}{x}\)

Answer:

\(\lim_\limits{x\to0}\frac{log_e(1+2x)}{x}\) 

\(\lim_\limits{x\to0}\frac{log_e(1+2x)}{2x}\times2\)

81. Evaluate the limits, if exist.

\(\lim_\limits{x\to0}\frac{log(1+x^3)}{sin^3x}\)

Answer:

\(\lim_\limits{x\to0}\frac{log(1+x^3)}{sin^3x}\)