Mensuration is a fundamental concept in mathematics that investigates the measurement of various geometric shapes and figures. It aids us in comprehending the dimensions of various two-dimensional and three-dimensional objects. A 2D shape has only two dimensions, length, and breadth, whereas a 3D figure has three dimensions: length, breadth, and height. The two most common parameters we measure for 2D shapes are area (A) and perimeter (P). Volume(V), total, lateral, and curved surface area are all calculated in 3D.

Learning mensuration formulas is difficult, especially for students who hate mathematics. Every class will have an entire chapter dedicated to calculating the area and perimeter of close planar figures. Mensuration is the topic of geometry in which geometrical figures and their parameters, which are as follows, must be measured.
- Length or breadth
- Area
- Perimeter
- Volume
- Lateral surface area
- Curved surface area
- Total surface area, etc.
Mensuration formulas for various 2-D and 3-D figures such as square, rectangle, triangle, circle, cuboid, cube, cylinder, sphere, cone, and hemisphere will be found. Mensuration formulas for Classes 6 to 10 can be found in this article. Before delving into the mensuration formulas, it's important to understand a few key terms.
Important Terms of Mensuration
You must have a thorough understanding of the important definition of mensuration in order to understand and implement geometry in everyday applications. The terms and their definitions are listed below.
| Terms |
Definitions |
| Closed Figures |
In geometry, a closed figure is an enclosed shape with all of its line segments or curves connected to one another. |
| Area |
The area of a two-dimensional close figure is the region it occupies. |
| Perimeter |
It is the total length of a closed figure along the boundary. |
| Circumference |
It is the total distance covered when you move around the circular path once along the boundary. |
| Surface Area |
It is the sum of the areas of faces of a solid figure. |
| Volume |
The region occupied by a three-dimensional solid figure is called its volume. |
| Frustum of a Cone |
When a small conical portion from the top of a right circular cone is removed, the resulting solid is called a Frustum of a cone. |
Difference Between 2d And 3d Shapes
| 2D Shapes |
3D Shapes |
| The shape which is surrounded by three or more straight lines in a plane would be referred to as a 2D shape |
The shape which is surrounded by a no. of surfaces or planes would be referred to as a 3D shape |
| They have no breadth or height |
These shapes are also termed solid shapes and have a combination of breadth and height |
| The perimeter and area of 2D shapes could be measured. |
The volume of these figures could be measured as CSA, LSA, or TSA. |
| Example: Square, Triangle, Rhombus, Trapezoid, Rectangle |
Example: Cube, Sphere, Cone, Hemisphere, Prism |
List of mensuration formula :
| 2D figures |
Figures |
Formula |
Mensuration formula for Triangle |
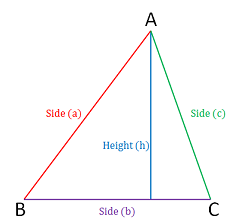 |
Perimeter= Sum of all sidesArea = 1/2 b x h
Area = \(\sqrt{s(s-a)(s-b)(s-c)}\)
a, b, c are sides of triangle.
Where s=\(\frac{a+b+c}{2}\)
Area=\(\frac{1}{2}\) (bxh) |
Mensuration formula for Equilateral Triangle |
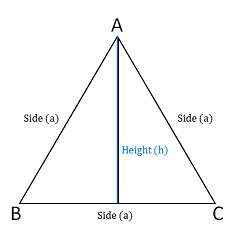 |
Perimeter= 3xSide
Area = \(\frac{\sqrt{3}}{4}\) (side)2 |
Mensuration
formula for Square |
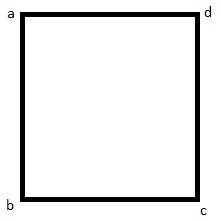 |
Perimeter: 4 x side
Area: (side)2 |
Mensuration
formula for Rectangle |
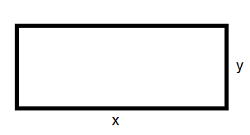 |
Perimeter= 2(length + breadth)
Area= length x breadth |
Mensuration
formula for Parallelogram |
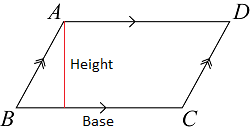 |
Perimeter= 2(1st side + 2nd side)
Area= base x height |
Mensuration
formula for Rhombus |
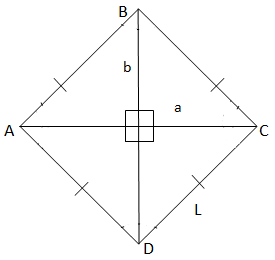 |
Perimeter= 4 x side
Area= \(\frac{1}{2}\) D1 x D2 |
Mensuration
formula for Trapezium |
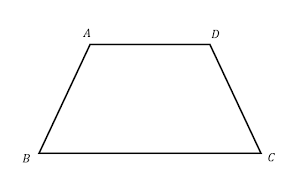 |
Perimeter= sum of all sides
Area= \(\frac{1}{2}\) (sum of parallel sides)x altitude |
Mensuration
formula for Circle |
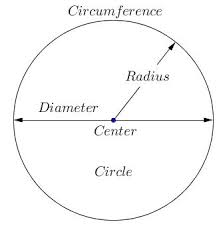 |
Circumference= 2πr
Area= πr2 (where r is radius) |
Mensuration
formula for Semicircle |
[caption id="attachment_3059" align="alignnone" width="236"]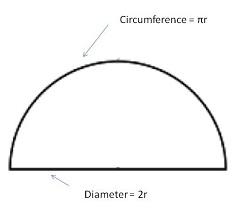 semi circle[/caption] semi circle[/caption] |
Perimeter= πr+2r
Area=\(\frac{1}{2}\)πr2 |
Mensuration formula for 3-D figures:
| 3 D figures |
Figures |
Formula |
Mensuration
formula for Cuboid |
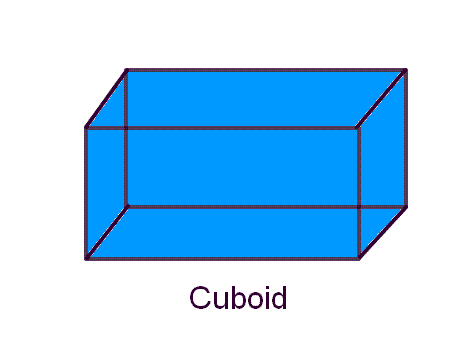 |
Surface Area: 2(lb+bh+lh)
Volume = L x B x H
Diagonal = \(\sqrt{l^{2}+b^{2}+h^{2}}\) |
Mensuration
formula for Cube |
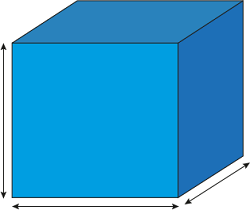 |
Surface Area= 6 x (side)2
Volume = (side)3
Diagonal = \(\sqrt{3}\)a |
Mensuration
formula forRight prism |
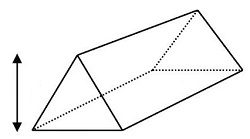 |
Lateral or curved surface area = perimeter of base x height
Total surface area = lateral surface area + 2(area of ends)
Volume= Area of base x Height |
Mensuration
formula for Right Circular cylinder |
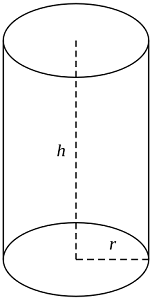 |
Lateral surface area = 2πrh
Total surface area= 2πrh + 2πr2
Volume= πr2h |
Mensuration
formula for Pyramid |
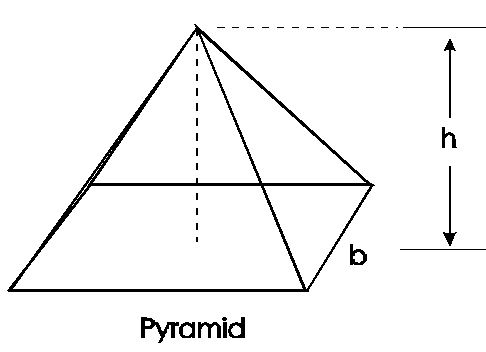 |
Lateral surface area= \(\frac{1}{2}\) perimeter of base x slant height
Total surface area= lateral surface area + area of base
Volume= \(\frac{1}{3}\) (area of base) x height |
Mensuration
formula for Sphere |
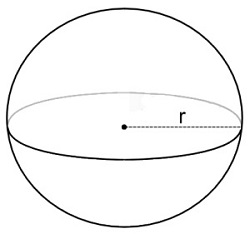 |
Surface area= 4πr2
Volume= \(\frac{4}{3}\)πr3 |
Mensuration
formula for Hemisphere |
 |
Lateral Surface area= 2πr2
Total surface area= 3πr2
Volume= \(\frac{2}{3}\)πr3 |
Mensuration
formula for Right circular cone |
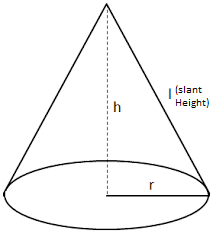 |
Slant Height= l = \(\sqrt{r^{2}+h^{2}}\)
Lateral surface area= πrl
Total surface area = πrl + πr2
Volume= \(\frac{1}{3}\) πr2h |
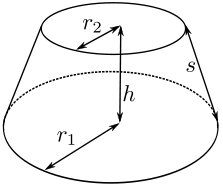
Mensuration
formula for Frustum of a cone |
[caption id="attachment_3077" align="alignnone" width="223"] formulas[/caption] formulas[/caption] |
Slant Height= l = \(\sqrt{{h}^{2}+ ({r}_1-{r}_2)^{2}}\)
Lateral surface area= πl(r1+r2)
Total surface area= πl(r1+r2) + πr12+ πr22
Volume= \(\frac{1}{3}\)πh(r12+r1r2+r22) |