Question

NCERT Solutions Class 12 Chemistry Chapter 3 Electrochemistry is developed by the expert mentor of the subject. These NCERT Solutions are made according to the latest syllabus provided by the CBSE.

NCERT Solutions Class 12 is designed in a concise manner that helps students understand difficult topics with ease.

• Electrochemistry – the branch of science that deals with the relationship between electricity and chemistry. Such chemical reaction which releases electric current is called electrochemical reactions.
  • The phenomenon of electrolysis produces a chemical change by electrical energy.
  • The production of electricity by spontaneous redox reaction by conversion of chemical energy into electrical energy.
• Electrochemical Cells – in spontaneous redox reaction which results in the conversion of chemical energy to electrical energy. These processes can also be reversed when electricity is applied to them. The process itself gives up some energy which is called Gibbs free energy. There are different types of electrochemical cells
  • Galvanic cell – it is the cell that converts chemical energy into electrical energy. This chemical and electrical energy exchange is done by a redox reaction. There are different compartments in the galvanic cell which contain the electrolytic solutions.
  • Electrolytic cells – these kinds of cells help change electrical energy into chemical energy. The electrolytic cell has an electrolytic solution in them. In the electrolytic cell, oxidation and reduction take place at the same time when the electric current is applied to it.
• Nernst Equation – the Nernst equation establishes the relationship between the potential cell to the standard potential and to activate electrically active cells.
• Corrosion – corrosion is the process by which the refined metal changes into a chemically stable oxide due to a chemical reaction. It is a slow process.

 NCERT Solutions Class 12 Chemistry has solutions of all kinds of NCERT intext questions, exercise questions, and also back of the chapter exercise questions.

Answer 1

NCERT Solutions Class 12 Chemistry Chapter 3 Electrochemistry

1. Arrange the following metals in the order in which they displace each other from the solution of their salts. Al, Cu, Fe, Mg and Zn

Answer:

The following is the order in which the given metals displace each other from the solution of their salts. 

Mg, Al, Zn, Fe, Cu

2. Given the standard electrode potentials, 

K⁺/K = −2.93V, Ag⁺/Ag = 0.80V, 

Hg²⁺/Hg = 0.79V 

Mg²⁺/Mg = −2.37 V, Cr³⁺/Cr = − 0.74V

Arrange these metals in their increasing order of reducing power.

Answer:

The lower the reduction potential, the higher is the reducing power. T

he given standard electrode potentials increase in the order of K⁺/K < Mg²⁺/Mg < Cr³⁺/Cr < Hg²⁺/Hg < Ag⁺/Ag. 

Hence, the reducing power of the given metals increases in the following order: 

Ag < Hg < Cr < Mg < K

3. Depict the galvanic cell in which the reaction Zn(s) + 2Ag⁺(aq) → Zn²⁺(aq) + 2Ag(s) takes place. Further show: 

(i) Which of the electrode is negatively charged? 

(ii) The carriers of the current in the cell. 

(iii) Individual reaction at each electrode.

Answer:

The galvanic cell in which the given reaction takes place is depicted as:

(i) Zn electrode (anode) is negatively charged. 

(ii) Ions are carriers of current in the cell and in the external circuit, current will flow from silver to zinc. 

(iii) The reaction taking place at the anode is given by,

Zn_(s) \(\longrightarrow\) Zn²⁺_(aq) + 2e^-

The reaction taking place at the cathode is given by,

Ag⁺_(aq) + e^- \(\longrightarrow\) Ag_(s)

4. Calculate the standard cell potentials of galvanic cells in which the following reactions take place: 

(i) 2Cr(s) + 3Cd²⁺(aq) → 2Cr³⁺(aq) + 3Cd 

(ii) Fe²⁺(aq) + Ag⁺(aq) → Fe³⁺(aq) + Ag(s) 

Calculate the ∆_rG^θ and equilibrium constant of the reactions.

Answer:

(i) \(E^\Theta _{cr^{3+}/cr} = 0.74 \,V\)

\(E^\Theta _{cd^{2+}/c4} = -0.4 0\,V\)

The galvanic cell of the given reaction is depicted as:

Now, the standard cell potential is

In the given equation, 

n = 6

F = 96487 C mol⁻¹

\(E^{\Theta}_{cell}\) = +0.34 V

Then, \(\Delta _rG^\Theta\) = −6 × 96487 C mol⁻¹ × 0.34 V 

= −196833.48 CV mol⁻¹ 

= −196833.48 J mol⁻¹ 

= −196.83 kJ mol⁻¹ 

Again,

\(\Delta _rG^\Theta\) = −RT ln K 

= 34.496 

\(\therefore\) K = antilog (34.496) = 3.13 × 10³⁴

(ii) \(E^\Theta_{Fe^{3+}/Fe^{2+}} = 0.77\,V\)

\(E^\Theta_{Ag^+/Ag}= 0.80\,V\)

The galvanic cell of the given reaction is depicted as:

Now, the standard cell potential is

Here, n = 1.

Then,

\(\Delta _rG^\Theta = -nFE^\Theta_{cell}\)

= −1 × 96487 C mol⁻¹ × 0.03 V

= −2894.61 J mol⁻¹ 

= −2.89 kJ mol⁻¹

Again,

= 0.5073 

\(\therefore\) K = antilog (0.5073)

= 3.2 (approximately)

5. Write the Nernst equation and emf of the following cells at 298 K:

(i) Mg(s) | Mg²⁺(0.001M) || Cu²⁺(0.0001 M) | Cu(s) 

(ii) Fe(s) | Fe²⁺(0.001M) || H⁺(1M)|H₂(g)(1bar) | Pt(s) 

(iii) Sn(s) | Sn²⁺(0.050 M) || H⁺(0.020 M) | H₂(g) (1 bar) | Pt(s) 

(iv) Pt(s) | Br₂(l) | Br⁻(0.010 M) || H⁺(0.030 M) | H₂(g) (1 bar) | Pt(s).

Answer:

(i) For the given reaction, the Nernst equation can be given as:

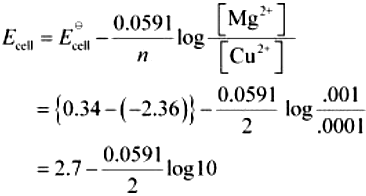
= 2.7 − 0.02955 

= 2.67 V (approximately) 

(ii) For the given reaction, the Nernst equation can be given as:

= 0.52865 V 

= 0.53 V (approximately) 

(iii) For the given reaction, the Nernst equation can be given as:

= 0.14 − 0.0295 × log125 

= 0.14 − 0.062 = 0.078 V 

= 0.08 V (approximately) 

(iv) For the given reaction, the Nernst equation can be given as:

6. In the button cells widely used in watches and other devices the following reaction takes place:

Determine \(\Delta _rG^\Theta\) and \(E^{\Theta}\) for the reaction.

Answer:

\(E^{\Theta}\) = 1.104 V

We know that,

\(\Delta _rG^\Theta= -nFE^\Theta\)

= −2 × 96487 × 1.04

= −213043.296 J

= −213.04 kJ

Answer 2

7. Define conductivity and molar conductivity for the solution of an electrolyte. Discuss their variation with concentration.

Answer:

Conductivity of a solution is defined as the conductance of a solution of 1 cm in length and area of cross-section 1 sq. cm. The inverse of resistivity is called conductivity or specific conductance. It is represented by the symbolκ. If ρ is resistivity, then we can write:

\(k =\frac 1p\)

The conductivity of a solution at any given concentration is the conductance (G) of one unit volume of solution kept between two platinum electrodes with the unit area of crosssection and at a distance of unit length.

i.e., \(G = k\frac al= k\times1 = k\)

(Since a = 1, l = 1) 

Conductivity always decreases with a decrease in concentration, both for weak and strong electrolytes. This is because the number of ions per unit volume that carry the current in a solution decreases with a decrease in concentration. 

Molar conductivity:

Molar conductivity of a solution at a given concentration is the conductance of volume V of a solution containing 1 mole of the electrolyte kept between two electrodes with the area of cross-section A and distance of unit length.

Λ_m ​= \(k\frac al\)

Now, l = 1 and A = V (volume containing 1 mole of the electrolyte).

Λ_m​ = kV

Molar conductivity increases with a decrease in concentration. This is because the total volume V of the solution containing one mole of the electrolyte increases on dilution. The variation of Λ_m​ with √c​ for strong and weak electrolytes is shown in the following plot :

8. The conductivity of 0.20 M solution of KCl at 298 K is 0.0248 Scm⁻¹. Calculate its molar conductivity.

Answer:

Given, 

κ = 0.0248 S cm⁻¹ 

c = 0.20 M

Molar conductivity, 

Λ_m = \(\frac{k\times1000}{c}=\frac{0.0248\times1000}{0.2}\)

= 124 Scm²mol⁻¹

9. The resistance of a conductivity cell containing 0.001M KCl solution at 298 K is 1500 Ω. What is the cell constant if the conductivity of 0.001M KCl solution at 298 K is 0.146 × 10^–3 S cm^–1

Answer:

Given,

Conductivity, k = 0.146 × 10⁻³ S cm−1

Resistance, R = 1500 Ω

Cell constant = k × R

= 0.146 × 10⁻³ × 1500

= 0.219 cm⁻¹

10. The conductivity of sodium chloride at 298 K has been determined at different concentrations and the results are given below:

Concentration/M            0.001     0.010     0.020     0.050     0.100

10² × k/S m⁻¹                      1.237     11.85     23.15     55.53     106.74

Calculate Λm for all concentrations and draw a plot between Λm and c^1/2. Find the value of 0 Λ m.

Answer:

Given,

κ = 1.237 × 10⁻² S m⁻¹, c = 0.001 M

Then, k = 1.237 × 10⁻⁴ S cm⁻¹, c^1/2 = 0.0316 M^1/2

= 123.7 S cm² mol⁻¹

Given,

κ = 11.85 × 10⁻² S m⁻¹, c = 0.010M

Then, κ = 11.85 × 10⁻⁴ S cm⁻¹, c^1/2 = 0.1 M^1/2

= 118.5 S cm² mol⁻¹

Given,

κ = 23.15 × 10⁻² S m⁻¹, c = 0.020 M

Then, κ = 23.15 × 10⁻⁴ S cm⁻¹, c^1/2 = 0.1414 M^1/2

= 115.8 S cm² mol⁻¹

Given,

κ = 55.53 × 10⁻² S m⁻¹, c = 0.050 M

Then, κ = 55.53 × 10⁻⁴ S cm⁻¹, c^1/2 = 0.2236 M^1/2

= 111.1 1 S cm² mol⁻¹

Given,

κ = 106.74 × 10⁻² S m⁻¹, c = 0.100 M

Then, κ = 106.74 × 10⁻⁴ S cm⁻¹, c^1/2 = 0.3162 M^1/2

= 106.74 S cm² mol⁻¹

Now, we have the following data:

Since the line interrupts Λ_m​ at 124.0 S cm² mol⁻¹, \(\Lambda^0_m\) =  124.0 S cm² mol⁻¹

11. Conductivity of 0.00241 M acetic acid is 7.896 × 10^–5 S cm^–1. Calculate its molar conductivity. If 0 Λ m for acetic acid is 390.5 S cm² mol^–1, what is its dissociation constant?

Answer:

Given, κ = 7.896 × 10⁻⁵ S m⁻¹ c

= 0.00241 mol L⁻¹

Then, molar conductivity,

\(\Lambda_m = \frac kc\)

= 32.76S cm² mol⁻¹

\(\Lambda^0_m\) = 390.5 S cm² mol⁻¹

Again,

Now,

= 0.084

Dissociation constant, K_α= \(\frac{c\alpha ^2}{(1-\alpha)}\) 

Answer 3

12. How much charge is required for the following reductions:

(i) 1 mol of Al³⁺ to Al?

(ii) 1 mol of Cu²⁺ to Cu?

(iii) 1 mol of MnO^-₄ to Mn²⁺?

Answer:

(i) Al³⁺ + 3e^- \(\longrightarrow\) Al

Required charge = 3 F 

= 3 × 96487 C 

= 289461 C

(ii) Cu²⁺ + 2e^- \(\longrightarrow\) Cu

Required charge = 2 F 

= 2 × 96487 C 

= 192974 C

(iii) MnO^-₄ \(\longrightarrow\) Mn²⁺

i.e., Mn⁷⁺ + 5e^- \(\longrightarrow\) Mn²⁺

Required charge = 5 F 

= 5 × 96487 C 

= 482435 C

13. How much electricity in terms of Faraday is required to produce

(i) 20.0 g of Ca from molten CaCl₂?

(ii) 40.0 g of Al from molten Al₂O₃?

Answer:

(i) According to the question,

Ca²⁺ + 2e^-1 \(\longrightarrow\) Ca

Electricity required to produce 40 g of calcium = 2 F

Therefore, electricity required to produce 20 g of calcium \(= \frac{2\times20}{40}F\)

= 1 F 

(ii) According to the question,

Al³⁺ + 3e^- \(\longrightarrow\) Al

Electricity required to produce 27 g of Al = 3 F

Therefore, electricity required to produce 40 g of Al \(=\frac{3\times40}{27}F\)

= 4.44 F

14. How much electricity is required in coulomb for the oxidation of 

(i) 1 mol of H₂O to O₂. 

(ii) 1 mol of FeO to Fe₂O₃.

Answer:

(i) According to the question,

Now, we can write:

Electricity required for the oxidation of 1 mol of H₂O to O₂ = 2 F

= 2 × 96487 C 

= 192974 C 

(ii) According to the question,

Fe²⁺ \(\longrightarrow\) Fe³⁺ + e^-1

Electricity required for the oxidation of 1 mol of FeO to Fe₂O₃ = 1 F 

= 96487 C

15. A solution of Ni(NO₃)₂ is electrolysed between platinum electrodes using a current of 5 amperes for 20 minutes. What mass of Ni is deposited at the cathode?

Answer:

Given, 

Current = 5A 

Time = 20 × 60 = 1200 s 

Charge = current × time 

= 5 × 1200 

= 6000 C 

According to the reaction,

Nickel deposited by 2 × 96487 C = 58.71 g

Therefore, nickel deposited by 6000 C \(= \frac{58.71\times6000}{2\times96487}g\)

= 1.825 g 

Hence, 1.825 g of nickel will be deposited at the cathode.

16. Three electrolytic cells A,B,C containing solutions of ZnSO₄, AgNO₃ and CuSO₄, respectively are connected in series. A steady current of 1.5 amperes was passed through them until 1.45 g of silver deposited at the cathode of cell B. How long did the current flow? What mass of copper and zinc were deposited?

Answer:

According to the reaction:

i.e., 108 g of Ag is deposited by 96487 C.

Therefore, 1.45 g of Ag is deposited by = \(\frac{96487\times1.45}{108}C\)

= 1295.43 C 

Given, 

Current = 1.5 A

Time = \(\frac{1295.43}{1.5}s\)

= 863.6 s 

= 864 s 

= 14.40 min 

Again,

i.e., 2 × 96487 C of charge deposit = 63.5 g of Cu 

Therefore, 1295.43 C of charge will deposit = \(\frac{63.5\times1295.43}{2\times96487}g\)

= 0.426 g of Cu

i.e., 2 × 96487 C of charge deposit = 65.4 g of Zn

Therefore, 1295.43 C of charge will deposit = \(\frac{65.4\times1295.43}{2\times96487}g\)

= 0.439 g of Zn

17. Using the standard electrode potentials given in Table 3.1, predict if the reaction between the following is feasible

(i) Fe³⁺(aq) and I^–(aq)

(ii) Ag⁺ (aq) and Cu(s)

(iii) Fe³⁺ (aq) and Br^– (aq)

(iv) Ag(s) and Fe³⁺ (aq)

(v) Br₂ (aq) and Fe²⁺ (aq).

Answer:

(i)

 

E^o  is positive, hence reaction is feasible.

(ii)

E^o  is positive, hence reaction is feasible.

(iii)

E^o  is positive, hence reaction is feasible.

(iv) 

E^o  is positive, hence reaction is feasible.

(v)

E^o  is positive, hence reaction is feasible.

Answer 4

18. Predict the products of electrolysis in each of the following:

(i) An aqueous solution of AgNO₃ with silver electrodes.

(ii) An aqueous solution of AgNO₃ with platinum electrodes.

(iii) A dilute solution of H₂SO₄ with platinum electrodes.

(iv) An aqueous solution of CuCl₂ with platinum electrodes.

Answer:

(i) At cathode:

The following reduction reactions compete to take place at the cathode.

The reaction with a higher value of E^o takes place at the cathode. Therefore, deposition of silver will take place at the cathode.

At anode:

The Ag anode is attacked by \(NO^+_3\) 

ions. Therefore, the silver electrode at the anode dissolves in the solution to form Ag⁺.

(ii) At cathode:

The following reduction reactions compete to take place at the cathode.

The reaction with a higher value of E^o takes place at the cathode. Therefore, deposition of silver will take place at the cathode.

At anode:

Since Pt electrodes are inert, the anode is not attacked by \(NO^+_3\)​ ions. Therefore, OH⁻ or \(NO^+_3\)​ ions can be oxidized at the anode. 

But OH⁻ ions having a lower discharge potential  and get preference and decompose to liberate O₂.

(iii) At the cathode, 

the following reduction reaction occurs to produce H₂ gas.

At the anode, the following processes are possible.

For dilute sulphuric acid, reaction (i) is preferred to produce O₂ gas. But for concentrated sulphuric acid, reaction (ii) occurs. 

(iv) At cathode: 

The following reduction reactions compete to take place at the cathode.

The reaction with a higher value of takes place at the cathode. Therefore, deposition of copper will take place at the cathode.

At anode:

The following oxidation reactions are possible at the anode.

At the anode, the reaction with a lower value of E^o is preferred. But due to the over potential of oxygen, Cl⁻ gets oxidized at the anode to produce Cl₂ gas.