Generation of sinusoidal AC voltage
Consider a rectangular coil of N turns placed in a uniform magnetic field as shown in the figure. The coil is rotating in the anticlockwise direction at an uniform angular velocity of ω rad/sec.




When the coil is in the vertical position, the flux linking the coil is zero because the plane of the coil is parallel to the direction of the magnetic field. Hence at this position, the emf induced in the coil is zero. When the coil moves by some angle in the anticlockwise direction, there is a rate of change of flux linking the coil and hence an emf is induced in the coil according to
Faradays Law. When the coil reaches the horizontal position, the flux linking the coil is maximum, and hence the emf induced is also maximum. When the coil further moves in the anticlockwise direction, the emf induced in the coil reduces. Next when the coil comes to the vertical position, the emf induced becomes zero. After that the same cycle repeats and the emf is induced in the opposite direction. When the coil completes one complete revolution, one cycle of AC voltage is generated.
The generation of sinusoidal AC voltage can also be explained using mathematical equations. Consider a rectangular coil of N turns placed in a uniform magnetic field in the position shown in the figure. The maximum flux linking the coil is in the downward direction as shown in the figure. This flux can be divided into two components, one component acting along the plane of the coil Φmaxsinωt and another component acting perpendicular to the plane of the coil Φmaxcosωt.
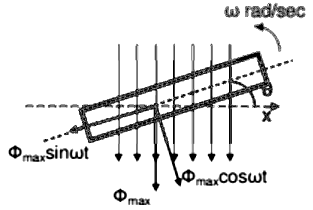
The component of flux acting along the plane of the coil does not induce any flux in the coil. Only the component acting perpendicular to the plane of the coil ie Φmaxcosωt induces an emf in the coil.
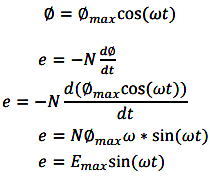
Hence the emf induced in the coil is a sinusoidal emf. This will induce a sinusoidal current in the circuit given by
\(i=i_{m}sin\,(wt)\)
Where
\(i\) is instantaneous value,
\(i_{m}\) maximum value
\(\omega\) is angular velocity