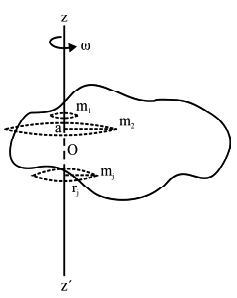
Fig shows a rigid body rotating about a fixed axis zoz´ with a constant angular speed ω. Consider rigid body as made up of point masses m1 , m2 ....... mj ....... mn as shown in Fig As rigid body rotates each point moves along a circle. The radius of circle equals the perpendicular distance rj of the jth mass from axis zoz´. The value of rj changes as j takes values 1, 2 ..... n. However every point mass completes one circle in same time T. T equals time taken by the rigid body to complete one full circle (or one revolution). Therefore angular speed of each point mass making the body is same. However the linear speed of each point mass in rigid body is different.
vj = The linear speed of jth mass = rjω .
We want to develope rotational dynamics in a manner similar to translational motion. Corresponding to every concept in Newtonian mechanics, there is a similar concept in rotational dynamics. The development of basics involves circular motion of each of the individual point masses. We will, therefore, describe basic concepts, using a single point mass and then generalize the concept for the rigid body.