Question

Show that the line 3x – 4y = 1 touches the circle x² + y² – 2x + 4y + 1 = 0 find the coordinates of the point of contact.

Answer 1

Centre and radius of circle x² + y² – 2x + 4y + 1 = 0 is (1,–2) and \(\sqrt{1 + 4-1}\) = 2 respectively. 

If the distance of a line 3x – 4y = 1 from the centre (1,–2) is equal to radius then the line touches or it is tangent to a circle.

Let point of contact be (x₁, y₁) then equation of tangent to a circle x² + y² – 2x + 4y + 1 = 0 is

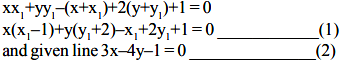
(1) and (2) are idenfical then comparing (1) and (2) we get