Question

Verify Cauchy’s mean value theorem for the following pairs of functions. 

(i) f (x) = x² + 3, g(x) = x³ + 1 in [1, 3].

(ii) f (x) = sinx, g(x) = cosx in [0, π/2]

(iii) f (x) = e^x , g(x) = e^–x in [a, b],

Answer 1

(i) We have Cauchy’s mean value theorem

Thus the theorem is verified. 

(ii) We have Cauchy’s mean value theorem

Clearly both f (x) and g (x) are continuous in [0, π/2] and differentiable in (0, π/2). Therefore from Cauchy’s mean value theorem

∴ f (x) and g (x) are continuous in [a, b] and differentiable in (a, b) 

and also g′ (x) ≠ 0 

∴ From Cauchy’s mean value theorem

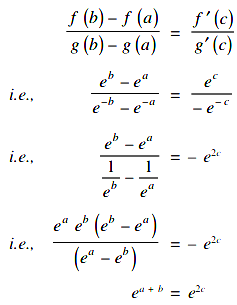
Hence Cauchy’s theorem holds good for the given functions.