correct option is B.


In the given system, the force acting on the block of mass 2M will have a force of 2F acting on it while the block M will have force F acting on it. On consideration of conditions in a state of maximum separation of the two blocks, the entire system comes to rest for a particular instant of time.
During this, the work done in the center of the mass frame will be zero. Therefore we get the total work done equation as Wspring+WF+W2F=0
. But, work done is a product of force and displacement for bodies and kinetic energy of springs.
Therefore,
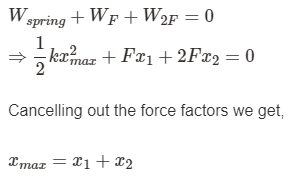
According to the given data, the masses of the two bodies are M and 2M
.
Therefore we can write it as Mx1=2Mx2
Upon reduction we get,
Mx1=2Mx2
⇒x1=2x2
Substituting the value of x1 in the displacement equation we get,

Substituting these values of x1 and x2 in the total energy equation of the system at rest we get,
