Question

Obtain Taylor's series expansion for log(cosx) about the point x = π/3 upto the fourth degree term.

Answer 1

The Taylor's series expansion a function f(x) about a point x = a is given by

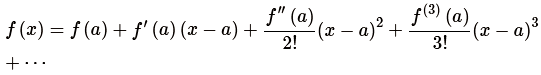
The given function is f(x) = log(cosx). We have to find the Taylor's series expansion of the given function upto the fourth degree term. So, we will compute upto the fourth derivative of the given function.

The value of the function at \(x = \frac \pi 3\) is \(f(\frac \pi 3) = \log(\cos \frac \pi 3) = \log (\frac 12)\).

The first derivative of f(x) is f′(x) = \(\frac 1{\cos x} \times (-\sin x)\). The value of the first derivative at \(x = \frac \pi 3\) is

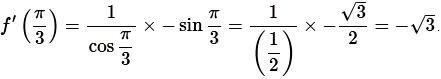
The second derivative of f(x) is f′′(x) = −sec²x. The value of the second derivative at \(x = \frac \pi 3\) is

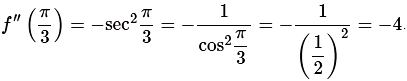
The third derivative of f(x) is f⁽³⁾(x) = −2sec²xtanx. The value of the second derivative at \(x = \frac \pi 3\) is

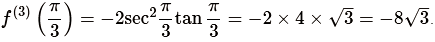
The fourth derivative of f(x) is f⁽⁴⁾(x) = 4sec²xtan²x + 2sec⁴x. The value of the second derivative at \(x = \frac \pi 3\) is

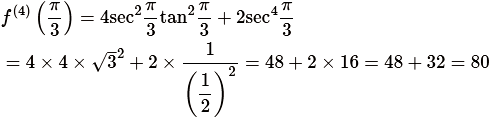
Now, substituting all these values in the Taylor's expansion series, we get

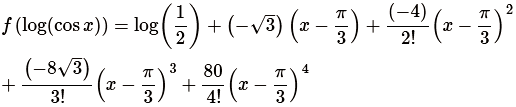
Simplifying the above equation, we get

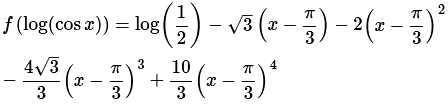
The above equation is the Taylor's series expansion up to the fourth degree term of the function f(x) = log(cosx).