Here is the detailed solution:
We know that
- In any triangle, all the angles add up to 180 degrees.
- In a triangle where two sides are the same length (isosceles triangle), the angles opposite those sides are also the same.

The proof involves working through a series of isosceles triangles. To begin, draw line segment BG such that angle CBG measures 20 degrees.
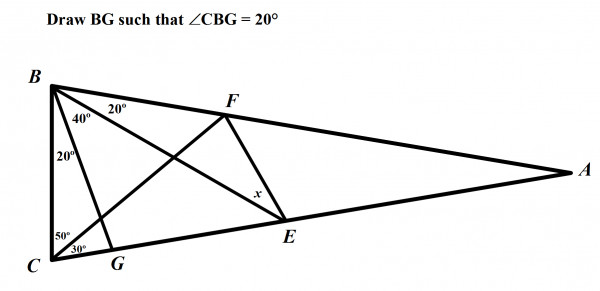
In triangle CBG, one angle is 20 degrees and another is 80 degrees.
Since the sum of the angles in a triangle is 180 degrees, we can solve for the third angle ∠CGB.
Therefore, ∠CGB = 180 - ∠CBG - ∠BCG
∠CGB = 180 - 20 - 80 = 80 degrees.
This implies that triangle CBG is indeed an isosceles triangle, meaning BC = BG.
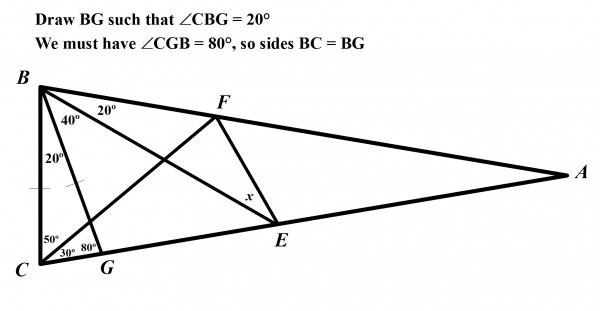
Angles CBG and BGE form a straight line so they must add up to 180 degrees. This means angle BGE is equal to 100 degrees.
Then, from triangle BGE, we can solve that ∠BEG = 180 - 40 - 100 = 40 degrees.
Triangle BGE has two angles equal to 40 degrees, so this is another isosceles triangle, so BG = GE.
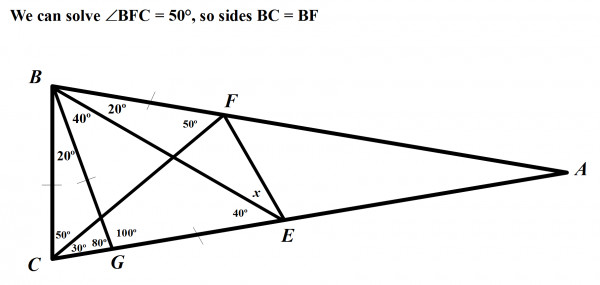
Then, from triangle BFC, we can solve that ∠BFC = 50 degrees, which means triangle BFC is another isosceles triangle. This means BF = BC.
We have proven BC = BG = GE = BF.
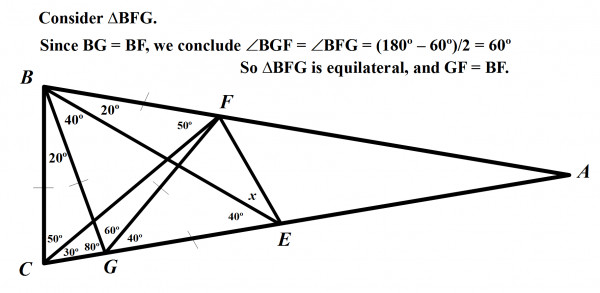
Now let's create another triangle BFG. Since BG = BF, we know the opposite angles must be equal.
The third angle in the triangle, ∠GBF, is 60 degrees, so the remaining angles have to be half of 180 – 60.
That is (180 – 60)/2 = 60 degrees.
In other words, all 3 angles are equal so BFG is an equilateral triangle. All of its sides must be equal, so GF = BF.
We know GF = GE, so we once again have an isosceles triangle, and we know the vertex angle is equal to 40 degrees. This means the remaining angles are one-half of 180 – 40, which is 70 degrees.
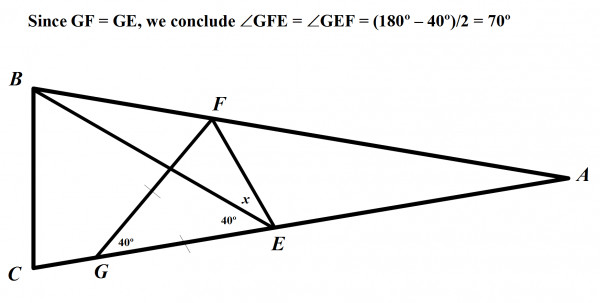
Finally, we know that 40 + x is equal to 70, so that means x = 30 degrees.
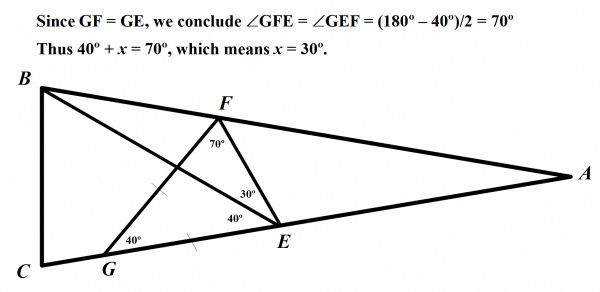
Hence, The value of x is 30 degrees.