व्यवरोध के रूप में दी गई असमिकाओं को समीकरण में व्यक्त करने पर
x + 2y = 120 …..(1)
x + y = 60 …(2)
x – 2y = 0 …(3)
असमिका x + 2y ≤ 120 द्वारा प्रदर्शित क्षेत्र –
रेखा x + 2y = 120 निर्देशी अक्षों को बिंदु A(120, 0) तथा B(0, 60) पर मिलती है अतः x + 2y = 120 के मानों के लिए सारणी
A(120, 0); B(0, 60)
बिंदुओं A(120, 0) तथा B(0, 60) को अंकित करते हुये आलेख खींचते हैं।असमिका में मूल बिंदु को प्रतिस्थापित करने पर,
0 + 2(0) = 0 ≤ 120
दी हुई असमिका को सन्तुष्ट करते है। अतः असमिको का सुसंगत हल क्षेत्र मूल बिंदु की ओर होगा।
असमिका x + y ≥ 60 द्वारा प्रदर्शित क्षेत्र –
रेखा x + y = 60 निर्देशी अक्षों के बिंदु C(60, 0) तथा (0, 60) पर मिलती है।
x + y = 60 के मानों के लिए सारणी
C(60, 0); D(0, 60)
बिंदुओं C(60, 0) और D(0, 60) को अंकित करते हुये रेखा का आलेख खींचते हैं।असमिका में मूल बिंदु को प्रतिस्थापित करने पर
0 + 0 ≥ 60
असमिका को सन्तुष्ट नहीं करते है। अतः असमिका का सुसंगत हल क्षेत्र मूल बिंदु के विपरीत ओर होता है।
असमिका x – 2y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
रेखा x – 2y = 0 निर्देशी अक्षों के बिंदु E(0, 0) तथा F(60, 30) पर मिलती है।
x – 2y = 0 के मानों के लिए सारणी
E(0, 0); F(60, 30)
बिंदुओं E(0, 0) तथा F(60, 30) को अंकित करते हुये रेखा को आलेख खींचते है।
असमिका में मूल बिंदु को प्रतिस्थापित करने पर,
0 – 2(0) = 0
असमिका को सन्तुष्ट करते हैं। अतः असमिका का सुसंगत हल मूल बिंदु की ओर होगा।
x ≥ 0,y ≥ 0 द्वारा प्रदर्शित क्षेत्र –
चूँकि प्रथम पाद में प्रत्येक बिंदु इन दोनों असमिकाओं को सन्तुष्ट करता है। अतः सुसंगत हल क्षेत्र प्रथम पाद में होगा।रेखा x + 2y = 120 तथा x + y = 60 के प्रतिच्छेद बिंदु के निर्देशांक (0, 60) होंगे।
रेखा x + 2y = 120 तथा x – 2y = 0 के प्रतिच्छेद बिंदु के निर्देशांक (60, 30) होंगे।
रेखा x + y = 60 तथा x – 2y = 0 के प्रतिच्छेद बिंदु के निर्देशांक (20, 40) हैं।
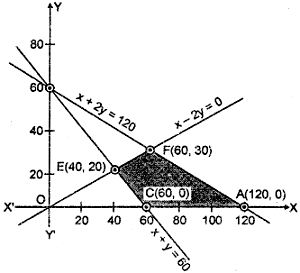
छायांकित क्षेत्र ACEF उपरोक्त असमिकाओं का उभयनिष्ठ क्षेत्र प्रदर्शित करता है। यह क्षेत्र दी गई रैखिक प्रोग्रामन समस्या का सुसंगत हल क्षेत्र है। इस क्षेत्र के कोनीय बिन्दुओं के निर्देशांक A(120, 0), C(60, 0), E(40, 20) तथा F(60, 30) हैं।
इन बिंदुओं पर उद्देश्य फलन कै मान निम्नलिखित सारणी में दिये गये है।
| बिन्द, |
x निर्देशांक |
y निर्देशांक |
उद्देश्य फलन Z = x+2y |
| A |
120 |
0 |
ZA=5(120)+10(0)=600 |
| C |
60 |
0 |
ZC=5(60)+10(0)=300 |
| E |
40 |
20 |
ZE=5(40)+10(20)=400 |
| F |
60 |
30 |
ZF=5(60)+10(30)=600 |
उपरोक्त सारणी से स्पष्ट है कि रैखिक प्रोग्रामन समस्या का इष्टतम हल बिंदु (60, 0) पर निम्नतम मान 300 तथा बिंदु A(120, 0) तथा F(60, 30) को मिलाने वाली रेखा के प्रत्येक बिंदु पर अधिकतम मान 600 है।
अत: बिंदु (60, 0) पर निम्नतम मान Z = 300
बिंदु (120, 0) तथा बिंदु (60, 30) वाली रेखा पर अधिकतम मान Z = 600.