Correct option is (B) \(\frac l3\)
Given data:
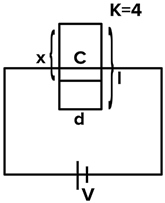
where length ‘l’, width ‘w’ and separation of plates is ‘d’
thickness of dielectric slab is also ‘d’ and its dielectric constant is K = 4.
\(\frac{U_{initial }}{U_{final}} = 2\)
where, U is the energy stored in the capacitor.
Finding the length at which initial energy will be twice of the stored energy:
Using the equation for energy stored in a capacitor,
\(U = \frac 12 CV^2\quad....(1)\)
Also using capacitance in parallel plate capacitor is given by
\(C = \varepsilon(lw /d)\)
where, C is the capacitance
\(\varepsilon\) is the permittivity of free space
A is area of the plate
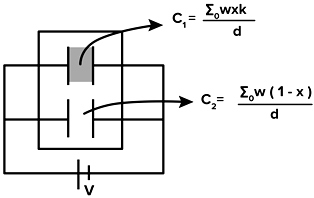
Comparing above equations and our given condition,
\(\frac{U_{initial }}{U_{final}} = 2\)
\(\Rightarrow\frac{C_1 + C_2}{C_{stored}} = 2\)
\(\Rightarrow\frac{kx + (l -x)}{l} = 2\)
\(\Rightarrow 4x + l - x = 2l\)
\(\Rightarrow x = \frac l3\)